研究出处：《DeFi Risk Assessment: MakerDAO Loan Portfolio Case》

  • 研究目的：评估MakerDAO借贷组合的相关风险。

  • 核心技术：构建一个基于多个布朗运动通道水平的风险模型——其中布朗运动代表不同的抵押品类型，通道水平对应用户的抵押品化比率。

  • 研究意义：提供了一种DeFi借贷项目的风险评估模型，可用于拓展epochChain团队的研究深度，结合前面已有诈骗代币检测技术，可以为后续开发山寨币质押借贷系统提供技术支持。

1. 背景介绍

MakerDAO协议是运行在以太坊区块链上的DeFi项目，其核心是通过DAI稳定币构建的借贷平台。DAI作为与美元软挂钩的ERC-20代币，依托抵押债务头寸（CDP）框架实现稳定性——用户可在智能合约"Vault"中锁定以太坊等加密货币作为抵押品生成DAI。协议参数（如影响借贷成本的稳定性费用、决定最低抵押要求的清算比率）由持有DAI的去中心化自治组织（DAO）投票决定，通过区块链技术实现智能合约管理的借贷环境，降低风险并提升金融服务可及性。

借款人在MakerDAO协议中的操作流程包括：创建Vault存放抵押品（如ETH是常用抵押品之一），通过预言机获取抵押品实时价格以确定可借贷DAI的额度；根据风险偏好选择不同借贷计划（如ETH-A、ETH-B等，各计划在利率、最低抵押率、清算罚款等参数上存在差异，ETH-A是最平衡且流行的计划）；基于实时估值和计划参数生成DAI，抵押品在还款前保持锁定状态。若Vault抵押品价值低于临界阈值，系统触发自动清算流程，通过DAI竞拍抵押品以偿还债务，未覆盖部分由MakerDAO承担损失，借款人需支付10%-33%的清算罚款，整个过程通过智能合约自动执行以减少人为干预和损失。

2. 相关研究

传统金融领域中，银行通过监管框架（如巴塞尔协议）和机器学习模型（如随机森林、线性回归）管理贷款风险，相关研究多基于私有数据，分析贷款组合分散化对风险和资本效率的影响。而DeFi借贷数据因公开透明的区块链特性，为风险评估研究提供了便利。

在DeFi风险研究中，部分学者运用现代投资组合理论分析借贷协议风险，或通过案例研究探讨DeFi与传统金融的互动。例如，针对MakerDAO协议的DAI稳定币稳定性、高抵押要求问题，以及Compound、Aave等平台的借贷活动，已有研究采用统计分析、线性回归等方法评估风险。然而，现有模型多针对系统整体风险，缺乏对个体债务违约相关性的量化分析，尤其在多种抵押品联合违约场景下的研究不足。本研究在已有单一资产模型基础上进行扩展，提出适用于多抵押品的风险评估框架，填补了DeFi项目特定风险模型的空白。

3. 数学模型

鉴于借款人可能持有多种类型的抵押品，研究着重处理多资产场景下的复杂性，并以两种特定抵押品作为典型案例进行分析。针对多资产相关性带来的挑战，提出将第二种资产的汇率建模为第一种资产布朗运动与独立布朗过程的线性组合。基于这一设定，研究进一步推导了两种资产联合违约的概率及其协方差，并计算了协议层面违约金额的概率分布，为多抵押品环境下的风险量化提供了理论框架。

3.1 基本符号

定义了Maker协议中贷款风险评估的核心符号与变量，构建数学模型的基础框架，具体包括：

  • 时间与抵押资产：贷款起始时间为$$t_0$$，终止时间$$T$$由清算、全额偿还或最长观察时间决定；抵押资产数量为$$a(t)$$，其变化通过分段常数函数记录（如存入、提取或清算事件）。

  • 债务与利息：债务$$d(t)$$随时间按指数累积利息，对数利率函数$$f(t)$$为分段常数，无干预时债务演化公式为$$d(t_2) = d(t_1) \cdot \exp(\int_{t_1}^{t_2} f(t)dt)$$。

  • 汇率与抵押率：抵押品对DAI的汇率$$e(t)$$由预言机提供，最低抵押率 $$r_{\text{min}}(t) > 1$$为分段线性函数；当前抵押率$$r(t) = \frac{e(t) \cdot a(t)}{d(t)}$$（债务为零时$$r(t) = +\infty$$），若 $$r(t) < r_{\text{min}}(t)$$则触发清算，期间借款人需持续支付利息。

3.2 违约概率

本节聚焦于DeFi贷款组合中违约概率（PD）的数学定义与建模，将MakerDAO协议中的“违约”明确为抵押品清算启动时刻，并通过定理1构建了双资产联合违约概率的计算框架，具体内容如下：

3.2.1. 违约的核心定义

违约触发条件：当用户抵押率$$r(t) = \frac{e(t) \cdot a(t)}{d(t)}$$低于协议设定的最低抵押率$$r_{\text{min}}(t)$$时，系统启动自动清算，该时刻定义为“违约”。

数学化表达：违约概率即布朗运动在时间区间$$(0, T]$$内跌破抵押率阈值对应的标准化水平$$x_{\text{min}}$$的概率$$(x_{\text{min}}$$由初始债务、抵押品价值和清算比率决定）。

3.2.2. 定理1：双资产联合违约概率模型

（1）核心假设

资产价格波动建模：

  • 第一种资产的标准化汇率对数收益率服从标准布朗运动$$B_t^1 \sim \mathcal{N}(0, t)$$，即$$\frac{1}{\sigma_1} \ln\left(\frac{e^1(t)}{e_0^1}\right) = B_t^1$$；

  • 第二种资产的汇率波动与第一种资产相关，建模为$$B_t^2 = \alpha B_t^1 + B_t^$$，其中$$B_t^$$是独立布朗运动（捕捉资产间相关性，$$\alpha$$为相关系数，$$\sigma_* = \frac{1}{\sqrt{1-\alpha^2}}$$）。

  • 简化条件：利率$$f_1 = f_2 = 0$$（忽略短期利息影响），最低抵押率$$r_{\text{min}}^1, r_{\text{min}}^2$$为常数，且初始抵押率均满足$$r(0) \geq r_{\text{min}}$$，用户在观察期内未调整抵押品或债务。

（2）联合违约概率公式

目标：计算两种资产在时间$$T$$内同时触发违约的概率，即$$P(T_{x_{\text{min}}^1} < T \cap T_{x_{\text{min}}^2} < T)$$，其中$$T_C$$为布朗运动首次到达阈值$$C$$的时间。

数学表达：$$PD(x_{\text{min}}^1, x_{\text{min}}^2) = \int_{-x_{\text{min}}^2}^0 \int_{-x_{\text{min}}^1}^0 \frac{\partial^2 F_{1,2}(a, b)}{\partial a \partial b} , da , db$$, 其中$$F_{1,2}(a, b)$$为联合分布函数，通过修正贝塞尔函数$$I_\mu(z)$$和角度参数$$\gamma, \theta_0$$描述相关布朗运动的联合行为，具体形式依赖于资产间的相关性系数$$\alpha$$。

3.2.3. 证明逻辑与关键推导

布朗运动对称性转换：利用布朗运动的对称性，将“跌破负向阈值”转换为“超过正向阈值”的联合事件，即：$$P(\inf_{0 \leq s \leq T} B_s^i \leq x_{\text{min}}^i) = P(\sup_{0 \leq s \leq T} B_s^i \geq -x_{\text{min}}^i)$$

引用现有研究成果：基于周春生（Chunsheng Zhou）关于多资产违约相关性的分析框架，通过二维积分计算联合事件的概率密度，最终推导得到包含资产相关性的联合违约概率公式。

3.2.4. 模型意义与局限性

理论贡献：首次在DeFi风险评估中引入多资产相关性建模，通过布朗运动的线性组合量化不同抵押品（如ETH与WBTC）的价格联动对违约风险的影响，为联合违约概率提供了可计算的数学框架。

假设约束：模型假设利率为零、用户行为固定且价格波动严格遵循布朗运动，忽略了现实中的利息变化、用户主动调整抵押品或债务，以及加密货币价格的跳跃式波动（如极端行情下的闪崩）。后续需通过蒙特卡洛模拟等方法结合真实数据校准，提升模型适用性。

3.3 风险评估

这里介绍基于定理1的双资产联合违约模型，进一步扩展至多资产场景，提出定理2以计算贷款组合的违约金额概率分布，构建DeFi贷款组合风险评估的完整框架，具体内容如下：

3.3.1. 核心目标与模型扩展

目标：量化整个协议层面的违约风险，即当多种抵押品同时或相继触发违约时，计算特定违约金额（如清算价值）的概率分布。

扩展逻辑：从定理1的双资产场景延伸至 (m) 种资产，考虑每种资产内用户按风险水平排序（风险从高到低），通过联合分布密度函数描述多资产价格波动的相关性。

3.3.2. 定理2：多资产违约金额概率分布

（1）关键假设

资产与用户结构：共有$$m$$种资产，第$$k$$种资产有$$n_k$$个用户，每个用户的抵押率阈值$$x_{\text{min}, i}^k$$按风险从高到低排序（$$x_0^k = 0 > x_1^k > \dots > x_{n_k}^k$$）。

价格与利率：第$$k$$种资产的标准化汇率对数收益率服从布朗运动$$E_t^k = \frac{1}{\sigma} \ln\left(\frac{e^k(t)}{e_0^k}\right)$$，利率$$f_k \geq 0$$为常数（允许非零利率）。

（2）核心公式

违约金额概率：对于给定的违约用户组合（如第$$k$$种资产中前$$n_k$$个用户违约），违约金额概率表示为多重积分，整合多资产布朗运动的联合分布密度$$f_m(x^1, \dots, x^m)$$：$$P(\text{DefaultCollaterals}) = \int_{-x_{i_m}^m}^{-x_{i_m+1}^m} \cdots \int_{-x_{i_1}^1}^{-x_{i_1+1}^1} f_m(x^1, \dots, x^m) , dx^1 \cdots dx^m$$,其中$$D_{i_k}^k = \sum_{j \leq i_k} d_j^k$$为第$$k$$种资产中前$$i_k$$个用户的债务总和。

简化场景：

  • 单资产（$$m=1$$）：违约金额概率为相邻风险水平的违约概率差，即$$P(D_i) = PD(x_i) - PD(x_{i+1})$$；

  • 双资产（$$m=2$$）：通过二维积分计算两种资产不同风险用户组合的联合违约概率。

（3）推论2.1：特定清算价值概率

当需要计算协议中所有资产违约金额之和等于某一特定值$$X$$的概率时，通过枚举所有可能的用户组合（$$\sum_{k=1}^m D_{i_k}^k = X$$），累加其联合违约概率：$$P(\text{LiquidationValue} = X) = \sum P(\text{DefaultCollaterals} : {D_{i_k}^k})$$

3.3.3. 模型特性与局限

理论贡献：

  • 首次将双资产联合违约模型扩展至多资产场景，支持按用户风险分层的违约金额概率计算；

  • 通过数学推导建立了从个体用户违约到协议整体风险的量化路径，为DeFi平台的风险储备设计和清算机制优化提供理论依据。

假设与挑战：

  • 假设同一资产内用户的抵押率阈值唯一，实际需先对用户按风险分组以满足该条件；

  • 仅理论推导了$$m=2$$时的联合分布，对于$$m>2$$的多资产场景，需依赖统计建模（如蒙特卡洛模拟）估计联合分布密度，增加了实际应用的复杂度；

  • 未考虑用户主动调整抵押品或债务、极端市场波动下的价格跳跃等现实因素，需结合真实数据进一步校准。

4. 数值实验

通过合成数据与真实数据实验，验证上面提出的布朗运动风险模型在DeFi贷款组合风险评估中的有效性，主要内容如下：

4.1. 合成数据实验

（1）布朗运动近似与相关性分析

Table 1: The Shapiro-Wilk test for the normality of BTC exchange rate increments for different time periods. The time series of the exchange rate from the beginning of BTC trading (2014-09-17) to the present (2024-03-29) is considered.

Table 2: The coefficients of the relationship of Brownian movements in the context of BTC-ETH.

正态性测试：对BTC汇率增量进行Shapiro-Wilk检验，发现不同时间区间（100天、3年、全周期）的p值均小于显著性水平（如全周期p值=2.72×10⁻³⁵），表明汇率增量不完全服从正态分布，布朗运动假设存在一定偏差，但作为金融建模的基础框架仍具参考价值。

相关性系数α：计算BTC与ETH的汇率相关性，发现α在0.79-0.84之间（如100天α=0.8007，3年α=0.8415），显示加密货币资产间存在强正相关，验证了模型中线性组合假设的合理性。

（2）违约概率验证：零利率假设的适用性

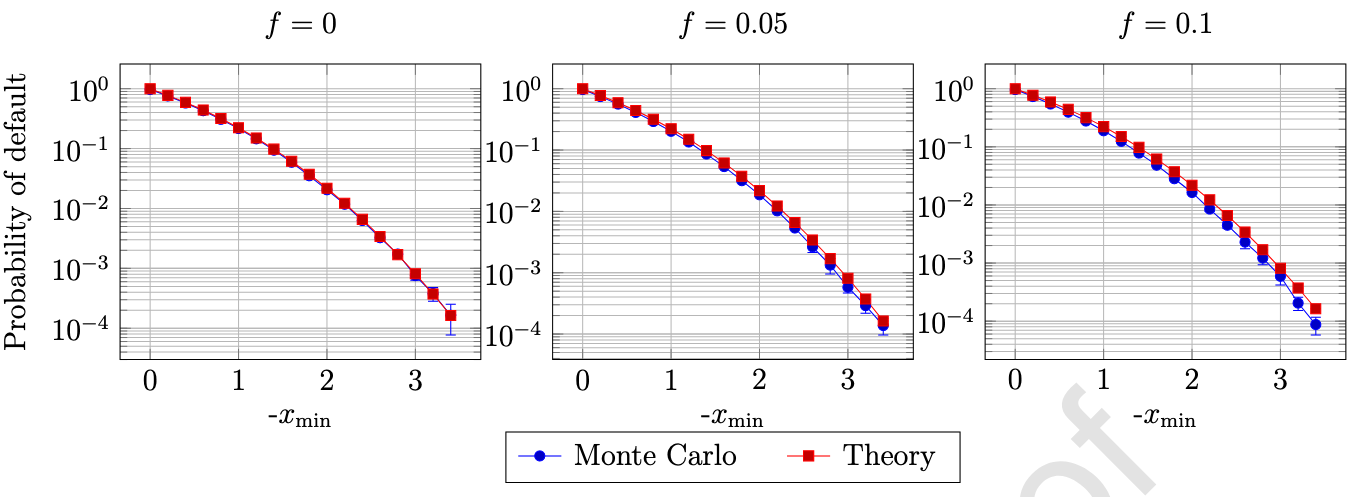
Figure 1: The results of comparing the theory with the Monte Carlo modulation method for different interest rates f , for x1 min = x2 min = xmin and α = 0.8.

Table 3: RMSE and MBE for theoretical and experimental data.

蒙特卡洛模拟：在不同利率（f=0、0.05、0.1）下，比较理论模型与模拟结果，发现零利率近似误差可忽略（如f=0.05时，根均方误差RMSE<0.01），支持模型在MakerDAO实际利率（1%-5%）场景下的适用性。

（3）风险评估结果

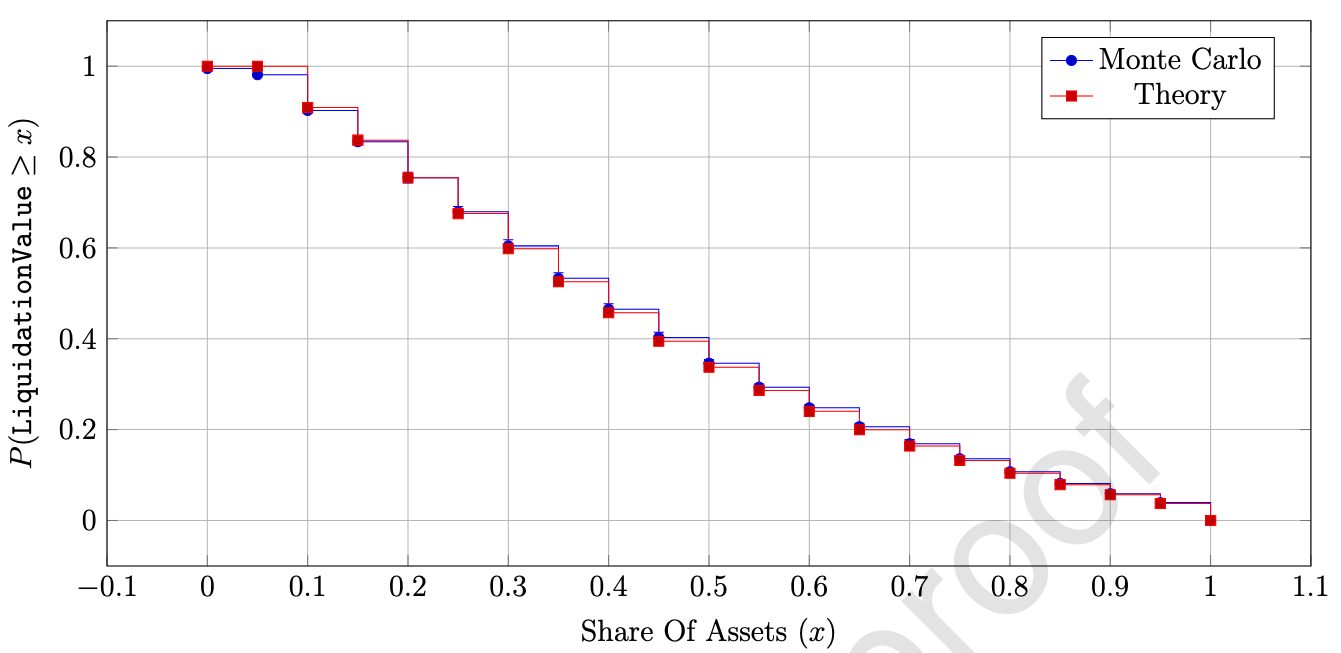
Figure 2: Complementary Cumulative Distribution Function for n = 20 users in each of two assets with equal levels, for x1 min = x2 min ∈ {−0.1k|k = 0..10}, f = 0.05 and α = 0.8.

通过互补累积分布函数（CCDF）展示20个用户的双资产组合（如ETH-A与WBTC-A）违约概率，结果显示随着抵押率阈值降低（$$-x_{min}$$增大），违约概率呈指数级上升，且理论曲线与模拟结果高度吻合，验证了定理2的风险计算框架。

4.2. 真实数据实验

（1）数据来源与资产选择

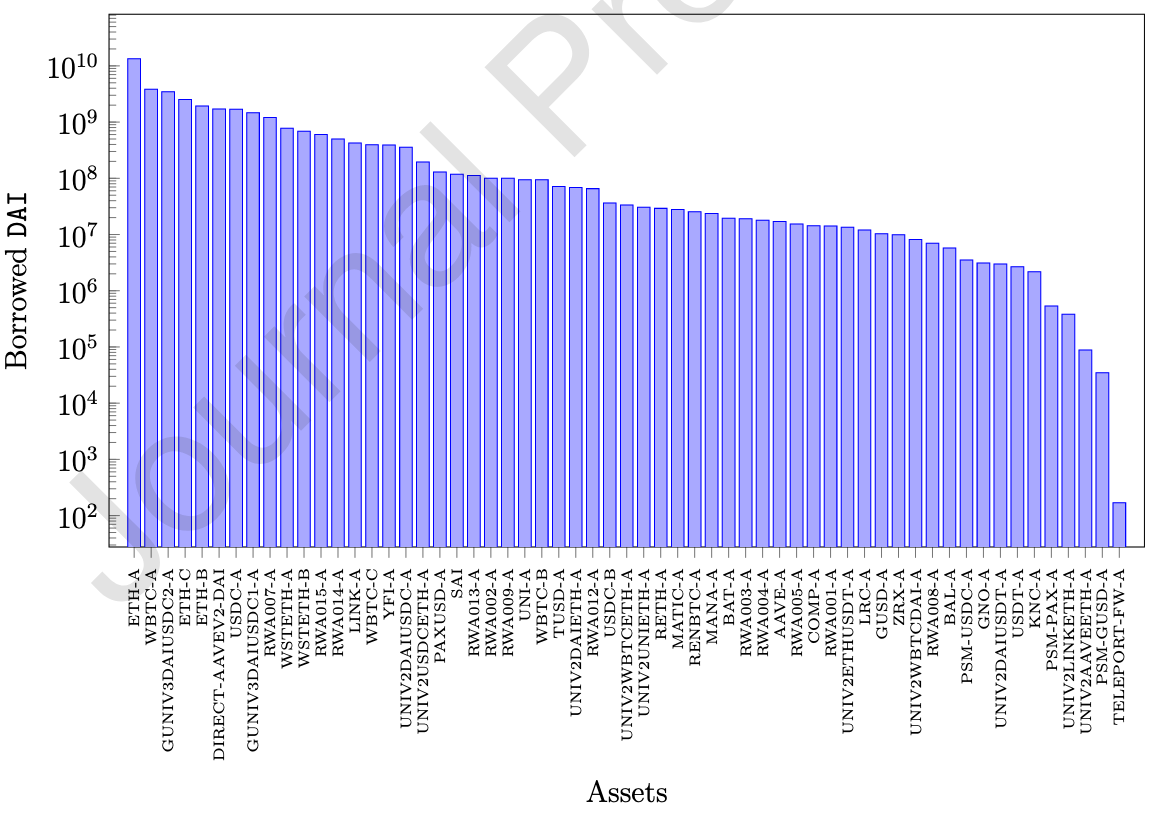
Figure 3: The total number of borrowed DAI for asset

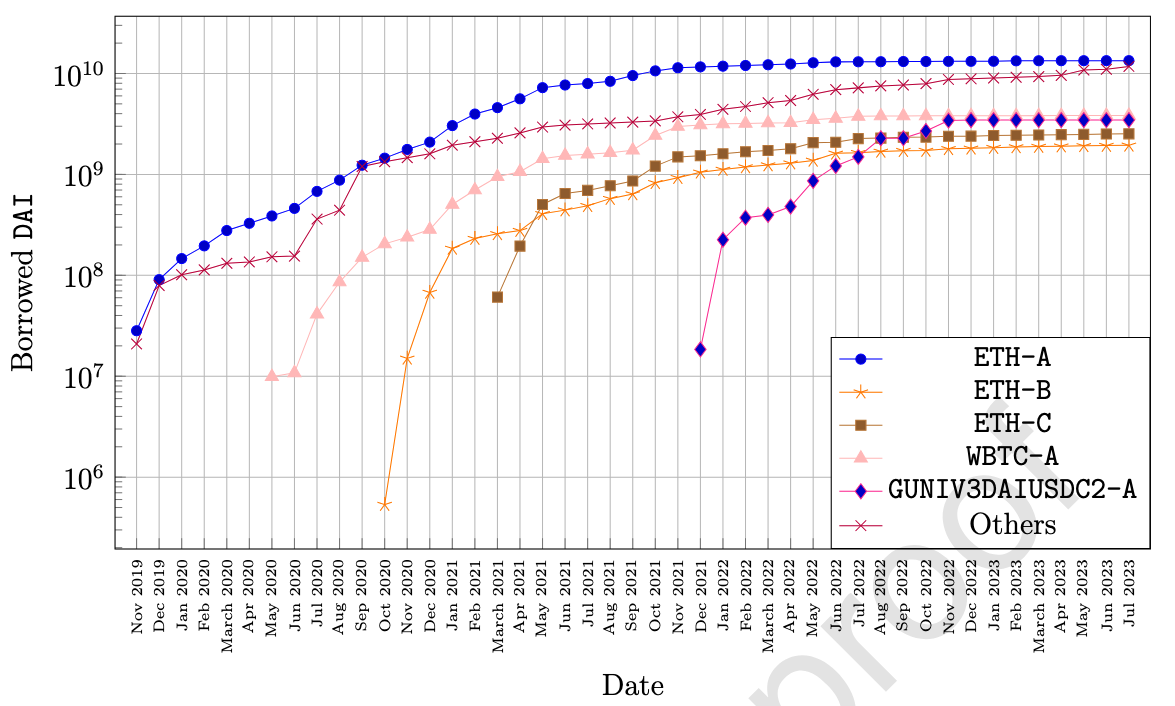
Figure 4: Dependence of borrowed DAI on date for each asset

数据来源：Google Big Query中MakerDAO协议的公开数据，涵盖2019年11月至2023年7月的ETH-A/B/C、WBTC-A、GUNIV3DAIUSDC2-A等主要抵押资产，包含用户操作（生成/偿还DAI、清算）、债务金额及抵押品参数。

关键参数：各资产的对数利率f(t)、汇率e(t)、最低抵押率$$r_{min}$$(t)随时间动态调整（如由预言机或DAO投票决定）。

（2）单一资产违约模型比较

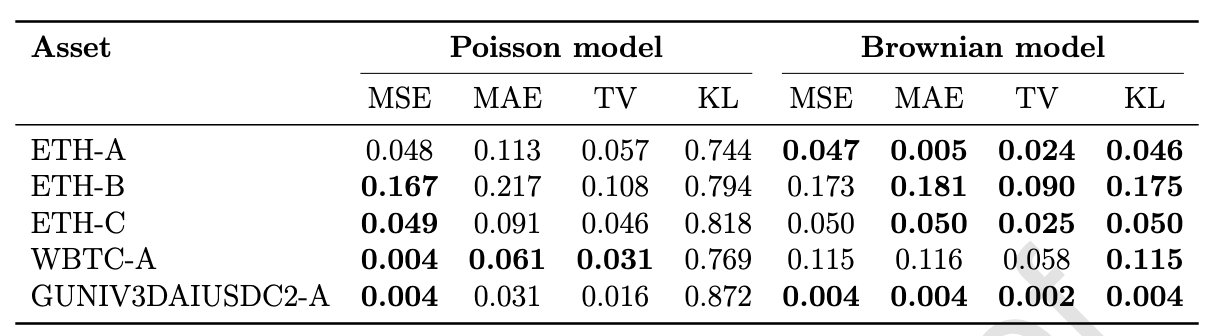
Table 4: Performance metrics for different mathematical models

布朗运动vs.泊松模型：

  • 指标：均方误差（MSE）、平均绝对误差（MAE）、总变异（TV）、Kullback-Leibler散度（KL）。

  • 结果：布朗运动模型在ETH-A、ETH-C等资产中表现更优（如ETH-A的MSE=0.047 vs. 泊松模型0.048），但WBTC-A中泊松模型因捕捉比特币价格跳跃风险更准确而占优，表明模型选择需结合资产特性。

（3）多资产联合违约风险

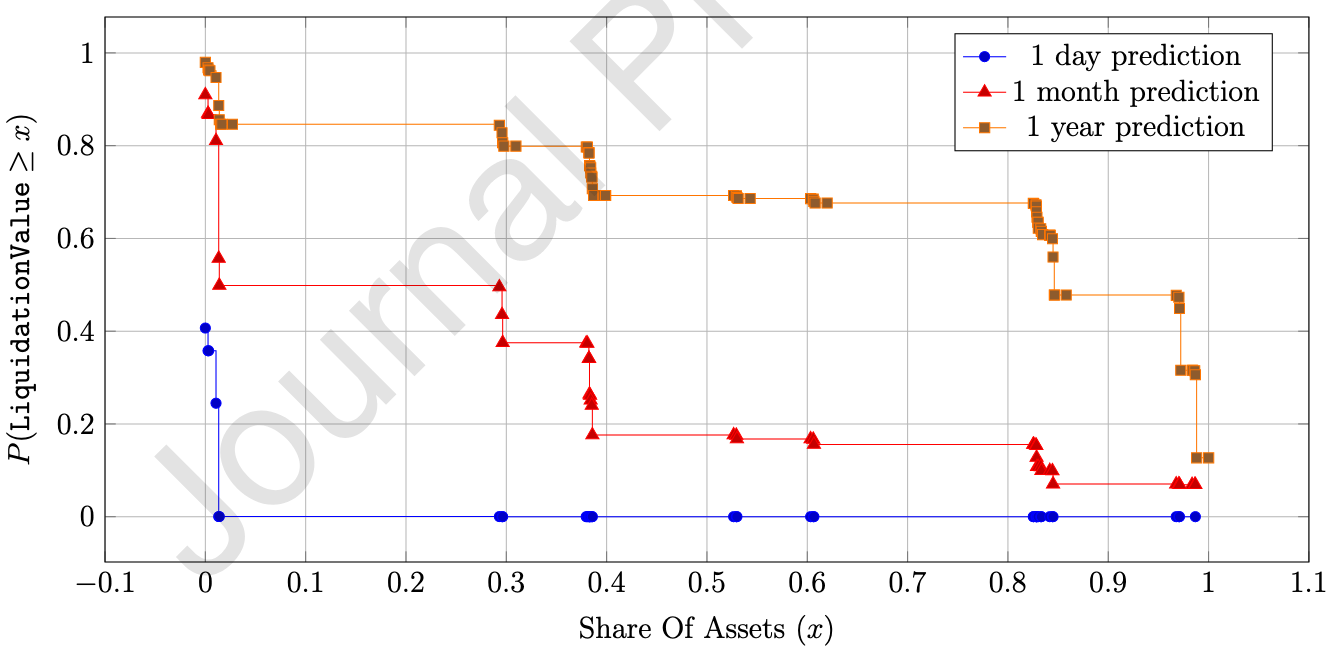
Figure 5: Probability of default of a share ≥ x of two assets (ETH-A and WBTC-A)

跨资产分析：以ETH-A和WBTC-A为例，计算不同时间区间（1天、1个月、1年）的违约概率，发现随着时间延长，违约概率显著上升（如1年时P(LiquidationValue≥x)比1天高30%-50%），符合“时间越长，价格波动突破阈值可能性越大”的逻辑。

实际意义：验证了模型对多资产相关性风险的捕捉能力，为MakerDAO等平台设置动态清算阈值和风险准备金提供数据支持。

5. 实验结论

本研究针对去中心化金融（DeFi）中MakerDAO贷款组合的风险评估问题，构建了基于多布朗运动通道水平的数学模型，将不同抵押品类型的价格波动通过布朗运动描述，以用户抵押品化比率作为通道水平，通过人工数据与2019年11月至2023年7月的真实数据实验，验证了模型在评估贷款组合风险方面的有效性。研究扩展了适用于DeFi贷款的数学模型，首次纳入多种抵押品并考虑其相关性，推导了双资产联合违约概率及多资产组合违约金额的概率分布，为DeFi场景下的风险量化提供了理论框架。尽管模型假设抵押品价格遵循布朗运动、利率固定且用户无主动干预等条件与现实存在一定差距，导致其在复杂市场环境中的适用性受限，但数值实验表明其能够有效捕捉资产相关性和长期风险趋势，展现了在单个DeFi项目中评估风险的潜力。研究强调，由于DeFi协议的独特性，需针对单个项目开发特定的风险评估模型，并建议未来结合价格跳跃过程、用户行为数据及机器学习方法进一步优化模型，同时鼓励对Aave、Compound等其他DeFi协议的风险评估展开探索，为推动DeFi行业的风险管控和可持续发展提供参考。

Mirror文章信息

Mirror原文：查看原文

作者地址：0x126988d50Cc7656C9bfbd07a564bf8525E0C7667

内容类型：application/json

应用名称：MirrorXYZ

内容摘要：vDIQIvRQkRrZwqPHlkeM9Gf9rvYdHe3k1kprigynfbI

原始内容摘要：izN4IEnSlfiWemxcdG-c5lmAncu6zjjXFzXppWmRmYc

区块高度：1668605

发布时间：2025-05-12 10:49:47