Highlights:

• How Impermanent loss (IL) and arbitrage cost appear

• All the costs of liquidity providers (LPs) on AMMs

• How BrownFi (as an innovative oracle-based AMM) mitigates IL & arbitrage loss, ensures LP gains

Impermanent Loss is common in all markets

Impermanent Loss (acronym IL, aka divergent loss) is simply the opportunity cost of adding liquidity into an AMM pool vs holding the individual tokens. IL disappears if and only if the price returns to the pool-entering price, otherwise IL becomes permanent loss. Formally, IL is measured by $$IL=\frac{PoolValue}{HoldValue}-1$$, being positive whenever price increases or decreases. In fact, divergent loss is a common phenomenon appearing in all financial markets, including CEXes and AMMs, at the side of market makers (MMs), or liquidity providers (LPs). However, MMs on CEXes can actively adapt to price changes very quickly, e.g. removing bids/asks with stale price and replacing them with updated orders surrounding the newly middle price. LPs on AMMs, unfortunately, have no way to do the similar actions, because they are passive to price change. Price of an AMM pool (constructed on constant product market making, aka CPMM model) is purely defined by the ratio of two token reserves, which is changed per swap by arbitrageurs or normal traders.

Why do LPs accept IL?

When providing liquidity on AMMs, LPs have an ONLY hope that accumulative trading fee can cover the loss, even help them gain.

The costs of liquidity provision other than IL

It is impossible to completely remove IL, even higher liquidity concentration causes higher IL (e.g. on Uniswap V3’s pools). Luckily, there are some ways to mitigate IL. For example, Balancer has modified the 50/50 inventory model of Uniswap V2 to build another version of CPMM with custom inventory ratio, hence reducing IL.

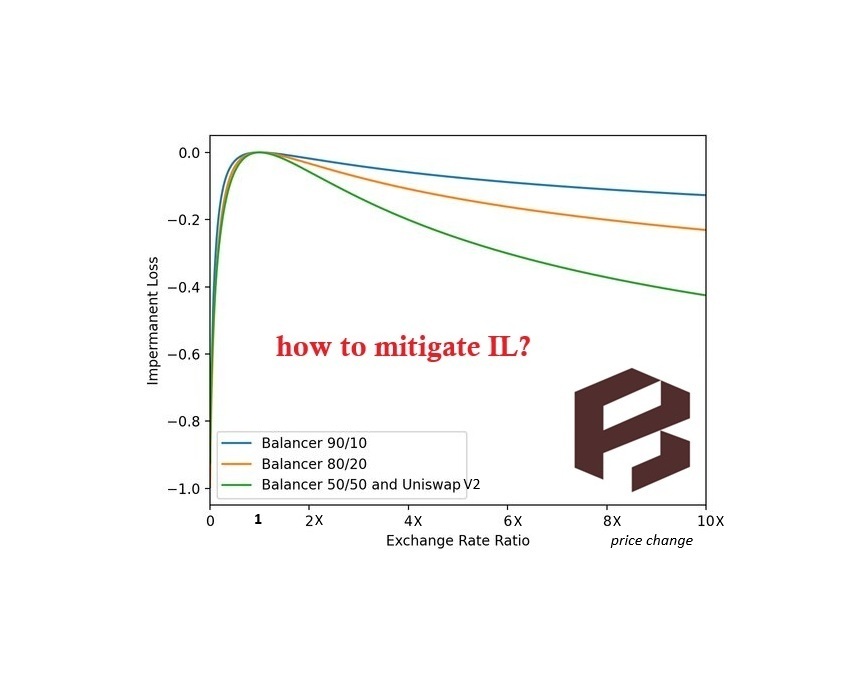
However, inventory imbalance, in turn, is an issue of Balancer, plus loss of adverse selection in the following. Interestingly, CPMM and impermanent loss are path-independent, i.e. IL is the same for any possible price trajectories (other than its initial and final values). Although IL is zero if the initial and final prices stay the same, that concept fails to isolate the adverse selection costs (caused by arbitrageurs) faced by LPs on most AMMs. In reality, there are always price discrepancies between CEXes (continuous price discovery in real-time) and DEXes (discrete price discovery per block time), giving opportunities for arbitrageurs to take profit at the expense of LPs. Then LP costs should be increasing in the number of opportunities for AMM arbitrage. And the frequency of such opportunities is very different if the price stays the same (no arbitrage) versus if it jumps around a lot (lots of arbitrage). Sorella Labs has tracked (in real time) that, since the Merge, LPs on Ethereum have lost over $750M due to arbitrate. Half of LPs on Uniswap V3 suffer losses due to high IL and out-of-range positions. In general, we have the loss versus rebalancing problem raised by A16Z researchers, which unites impermanent loss and arbitrage cost as the costs of liquidity provision.

How oracle-based BrownFi AMM protects LPs?

Suppose an AMM pool (e.g. on Uniswap V2 and V3 with bonding curve $$x* y=k$$ for both) has 1 ETH and 1000 USDC. Suppose further that at a very good moment for ETH, the market price jumps from $1000 to $4000. This requires a swap of 1000 USDC plus 3 USDC trading fee to receive 0.5 ETH, according to Uniswap V2 (roughly ignoring a very slight price difference of the post-trade pool ratio 0.5 ETH : 2003 USDC). In this case, the decision to provide liquidity would have doubled your money from a $2000-value portfolio on deposit to a $4003-value one upon withdrawal (0.5 ETH and 2003 USDC).

If you sell 0.5 ETH on a high liquid CEX (e.g. Binance) at $4000, after that, your portfolio (0.5 ETH, 3000 USDC) value is $5000 dollars, equal holding portfolio. Consequently, providing liquidity on the AMM cause your loss of $997.

Now, let’s see how BrownFi works with the initial (1 ETH, 1000 USDC) reserve and the same trade of buying $$dx=0.5$$ ETH at the market price $4000. With a high liquidity concentration (parameter Kappa $$K=0.001$$), BrownFi’s pricing formulas read.

• Price impact factor $$R=K\times \frac{dx}{x-dx}=0.001 \times \frac{0.5}{1-0.5}=0.001$$

• Trading price $$P_t=4000(1+R/2)=4002$$, so paying $$dy=dx * P_t=2001$$ USDC, plus 6 USDC trading fee.

Thus, the LP portfolio on BrownFi AMM is (0.5 ETH and 3007 USDC) valued $5007 dollars, higher than holding. Without trading fee, what is $1 dollar greater than the holding portfolio? It is exactly the price impact cost BrownFi AMM charges per trade. It is LPs’ incentives (plus trading fee) to provide liquidity.

You may ask “trading on BrownFi AMM is worse than Uniswap V2” (because paying USDC doubly). NO. In fact, the trade on Uniswap is made by a smart arbitrageur who has the best tools to hunt profitable opportunities effectively upon price discrepancies at the expense of LPs. Let’s see next.

Now, assume the 2nd trade that the market price stays the same at $4000, and a normal trader wanna buy 0.1 ETH. The Uniswap pool, after the first trade, has 0.5 ETH and 2003 USDC. Solving by $$xy=k$$ formula $$(0.5 – 0.1)*(2003 + dy)=0.5 * 2003, \Rightarrow dy=500.75$$ plus 1.5 USDC trading fee. The trader pays 502.25 USDC, meaning 25% more expensive than the market price. The post-trade pool is 0.4 ETH and 2505.25 USDC, priced $6263.125 per ETH, much higher than the market price. This, again, gives an arbitrage opportunity to sell 0.1 ETH back to the pool (the 3rd trade), receiving 500.8 USDC, roughly taking 100 USDC profit at the expense of the previous trader. Eventually, the portfolio on Uniswap pool is (0.5 ETH and 2004.25 USDC) valued $4004.25 with negligible price difference, mostly same as the value after the 1st trade.

After the first trade, BrownFi AMM pool has 0.5 ETH and 3005 USDC. Then we have the 2nd trade (buying $$dx=0.1$$ ETH)

• Price impact factor $$R=K\times \frac{dx}{x-dx}=0.001\times\frac{0.1}{0.5-0.1}=0.00025$$

• Trading price $$P_t=4000(1+R/2)=4001$$, so paying $$dy=dx * P_t=400.1$$ USDC with negligible slippage, plus 1.2 USDC trading fee.

The portfolio on BrownFi AMM pool is now (0.4 ETH and 3408 USDC) valued $5008, still higher than holding.

Without loss of generality, the previous examples take an extreme price volatility (for easy computation & reading) to illustrate that Uniswap V2 and V3 models are exposed to both IL and arbitrage loss. Arbitrageurs take profits at the expense of either LPs or ordinary traders. In contrast, BrownFi is an oracle-based AMM, always offering trade at market price plus a price impact cost. Therefore, by eliminating arbitrage opportunities, BrownFi AMM mitigates overall loss and guarantees gains of LPs.

The following table summarizes the state changes from the initial portfolio of 1 ETH, 1000 USDC throughout 3 trades with the market price of 1 ETH = $4000 dollars, reaching final state. With this setting, Uniswap V2 & V3 are identical by using the same formula $$x\times y=k$$. Note that the holding value is $5000 and 0.3% trading fee is applied on USDC side of the two AMMs. If you choose a lower price (e.g. $2000 or $500), the absolute values change with small numbers of many decimals, but the relative quantities and implied properties are still the same. Thus, it doesn’t affect our conclusions on the nature of exchange models.

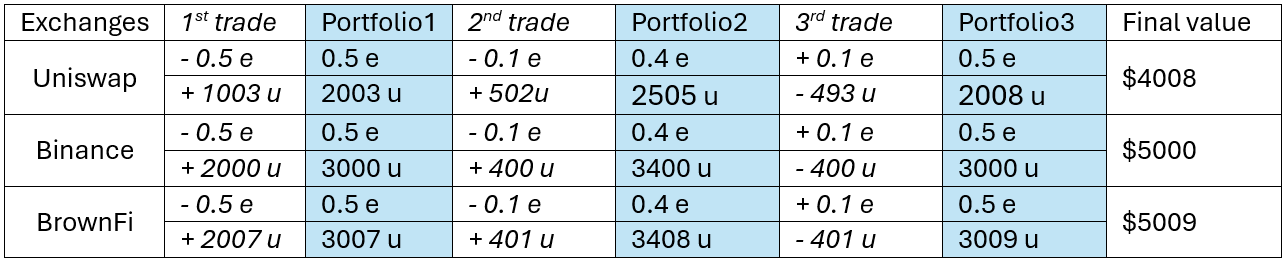
Is BrownFi AMM better Uniswap?

It is worth clarifying that impermanent loss is only suitable for Uniswap and AMMs (e.g. Balancer, Shushiswap, Pancakeswap) using CPMM models, which offer independent price discovery mechanisms. Regarding BrownFi and other oracle-based AMMs (e.g. Dodo, Lifinity) possessing price-ambience, a universal consideration of LP costs, including arbitrage cost, is more precise. In the table above, BrownFi outperforms CEX and holding with a small gain +$9 for LPs, while Uniswap makes them a huge loss of -$992. In practice, under market dynamics, market making is more complicated with many scenarios. However, one thing is still valid that BrownFi, in general, all oracle-based AMMs, are resistant to arbitrage and sandwich attacks, thus ensure better gains for LPs. Don’t get me wrong, Uniswap and CPMM-AMMs discover price independently, hence are the only choice for tokens unlisted on CEXes. BrownFi only works if a reliable price source is available. Uniswap and CPMM-AMMs play a vital role in decentralized finance (DeFi). BrownFi, an oracle-based AMM, is a complementary solution to the CPMM-based AMM models. If oracle-price is reliable and dominant (e.g. tokens listed on CEXes with good liquidity), BrownFi AMM is potential to outperform Uniswap V3. Readers can find a comprehensive article about oracle-based AMMs here.

Contact us

Website, Twitter, Telegram, blog