Episode 8: Liệu chúng ta đã biết LPing đúng cách?

Chào anh chị em,

Hôm nay chúng ta hãy bàn về một chủ đề, đó là liệu ta đã biết LPing đúng cách và tạo ra lợi nhuận bền vững. Dạo gần đây do tôi có tham gia vào 1 dự án AMM là BrownFi, nên tôi cũng được vỡ ra khá nhiều về cách thức hoạt động của Market Maker (MM) truyền thống thông qua Limit Order Book (LOB). Từ đó, khi tham chiếu vào các model AMM mà tôi vẫn chơi LPing trên blockchain, tôi mới nhận ra rằng bấy lâu nay mình “Chơi” mà thực sự không “hiểu bản chất” vấn đề, do đó đã tạo nên nhiều những tổn thất “không đáng có”. Trong bài viết này, anh chị em hãy cùng tôi quay về tư duy nguyên bản, và lật lại vấn đề về việc phân bổ thanh khoản (liquidity distribution) từ mô hình LOB truyền thống lẫn AMM (mà điển hình nhất là model CPMM của Uniswap V2 và CLMM của Uniswap V3), để xem có thể đúc rút được những insight gì khiến cho chúng ta có thể nâng cao skill khi chơi LPing lên.

Nào, hãy bắt đầu thôi!

LOB là gì?

Các sàn giao dịch hiện nay phần lớn vận hành xung quanh 1 sổ lệnh (order book) bao gồm các lệnh chờ ‘limit order’ đợi để được khớp. Một lệnh limit order thường thể hiện ý muốn bán (gọi là ‘ask’ order) hoặc ý muốn mua (gọi là ‘bid’ order) một số lượng token nhất định (gọi là ‘order size’) tại một giá nhất định. Một lệnh limit order vừa mới được đặt sẽ được khớp với các lệnh limit order khác có giá gần nhất trong sổ. Nếu không có lệnh nào khớp với giá đó, những lệnh chưa được khớp sẽ được thêm vào sổ và chờ được khớp với các lệnh khác trong tương lai. Trader cũng có thể submit 1 lệnh mua ngay (gọi là ‘market order’) thể hiện ý định sẵn sàng khớp với giá limit order tốt nhất hiện có trong sổ. Dạng market order này sẽ được khớp ngay lập tức bởi nó được coi như giá rẻ nhất cho bên mua, hoặc là giá cao nhất cho bên bán.

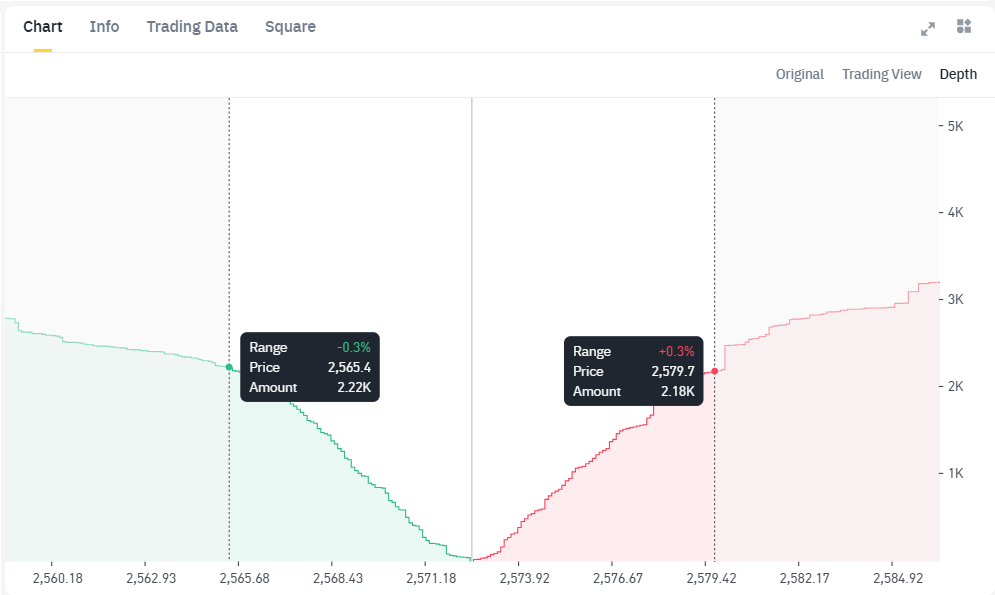
Ví dụ với phân bổ liquidity của order book cặp ETH-USDT trên sàn Binance, ta có thể nhận ra hình dạng của Order book có dạng V-shape. Nơi mà ngay tại market price có lượng thanh khoản rất ít, và càng dịch chuyển ra xa thì sẽ có càng dày lệnh chờ mua (bên trái) và lệnh chờ bán (bên phải) hơn.

Ví dụ:

• Tại tick giá ETH = $2,565.4 (-0.3%) có lượng USDT sẵn sàng mua 2.22k ETH.

• Tại tick giá ETH = $2.579.7 (+0.3%) có 2.18k ETH sẵng sàng bán.

Order book trên các sàn CEX có dạng V-shape là điều dễ hiểu, bởi vì người mua thì sẽ luôn muốn mặc cả để mua với giá rẻ hơn, còn người bán thì sẽ luôn muốn mặc cả để có thể bán đắt hơn. Và khoảng chênh lệch giữa 2 lệnh limited buy và limited sell gần nhất được gọi là spread (độ giãn).

Và các MM truyền thống kiếm lợi nhuận được là nhờ vào spread này, do trading fees thì lại thuộc về các sàn CEX. Điều này hoàn toàn ngược lại với các sàn DEX như Uniswap, nơi mà spread bằng 0 (do lệnh buy/sell của Taker đều được khớp với 1 giá duy nhất theo công thức $$p=y/x$$), do vậy MM chỉ kiếm lợi nhuận từ trading fees.

Model LOB này đã tồn tại và hoạt động hiệu quả trên các sàn giao dịch từ xa xưa cho tới tận bầy giờ. Ta có thể dễ dàng thấy các mức giá buy/sell được hiển thị theo thời gian thực, và giúp trader có cái nhìn tổng quan để ra quyết định mua bán dễ dàng hơn. Tuy nhiên, LOB rất khó triển khai trên blockchain cho các sàn DEX. Dữ liệu về LOB thường quá lớn để có thể lưu trên blockchain, và với tần suất update liên tục các mức giá sẽ khiến đội gas cost lên. Ngoài ra, việc khớp lệnh thông qua LOB trên blockchain không thể thực hiện ngay tức thì và với hàng triệu lệnh/giây như các sàn CEX, ngay kể cả với các giải pháp blockchain L2 như Arbitrum, Optimism hay với các L1 chuyên biệt như HyperLiquid hay dYdX.

Do vậy, các DEX thường hay chạy theo Model AMM nơi mà nghiệp vụ pricing (xác định tỷ giá giữa 2 token trong pool) được thực hiện thông qua công thức toán học, thay vì thông qua LOB phản ảnh đúng nhu cầu buy/sell của các bên maker/taker trên thực tế. Điển hình là các bên như Uniswap với model CPMM (x*y=k), hoặc Balancer, Curve v.v…

Vậy cách thức phân bổ thanh khoản trong các AMM này như thế nào? Liệu chúng có mặt mạnh và yếu nào so với model LOB thông thường?

Phân bổ thanh khoản của model CPMM (Uniswap V2)

Xét với pair ETH-USDC trong đó x là balance của ETH, và y là balance USDC. Tại bất kỳ thời điểm nào, thì pool ETH-USDC trong Uniswap V2 luôn hoạt động theo công thức sau:

$$$
x*y=L^2
$$$

Trong đó, L là 1 hằng số.

Và của ETH so với USDC được xác định theo công thức:

$$$
p=\frac{y}{x}
$$$

Như vậy, khi giá của ETH thay đổi, thì từ 2 tham số L và p ta luôn có thể xác định được chính xác (x,y) tại mức giá đó như sau:

$$$
\begin{cases}
x&=\frac{L}{\sqrt{p}} \
y&=L*\sqrt{p}
\end{cases}
$$$

Được inspired bởi model phân bổ liquidity của Order book trong truyền thống bên trên, ta sẽ cùng đi sâu vào tìm hiểu xem nếu AMM có 1 LOB thì hình dáng và phân bổ liquidity của nó trông như thế nào.

Phân bổ liquidity của ETH

Tại mỗi điểm giá $$ p_0$$ bất kỳ, ta sẽ dễ dàng nhận thấy lượng liquidity của 2 token trong pool $$ (x_0,y_0)$$ không hề tĩnh, mà sẽ được tính toán lại với giá trị là $$ (L/\sqrt{p_0},L\sqrt{p_0})$$. Như vậy, ta có thể suy ra được với mỗi điểm giá $$ p_0$$ sẽ cho ra một phân bổ liquidity mới tương ứng.

Giả sử phân bổ liquidity của ETH và USDC tại $$ p_0$$ có hình dạng bất kỳ như dưới đây:

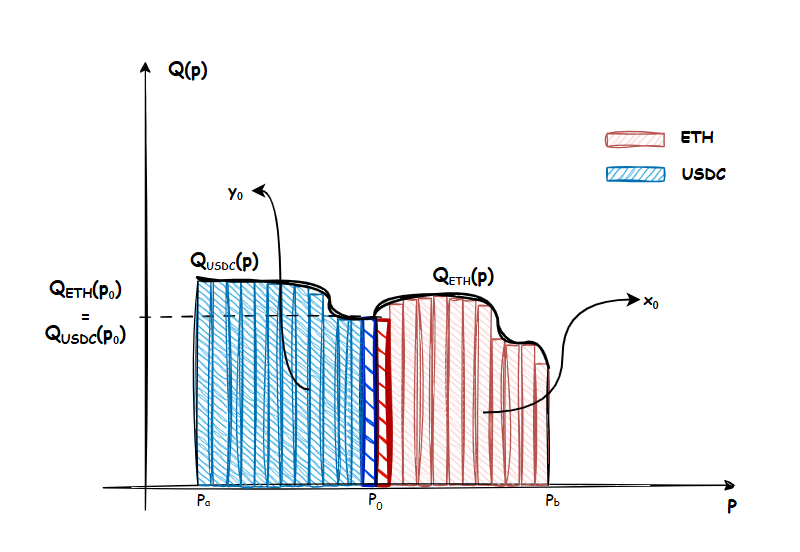
Trong đó:

• $$ Q_{ETH}(p)$$ biểu diễn share của ETH bên ask (chờ bán), phân bổ trong mỗi tick giá $$ p\in (p_0,p_b)$$. Đối với pool ETH-USDC thì số share này chính bằng số lượng ETH.

• $$ Q_{USDC}(p)$$ biểu diễn share của ETH bên bid (chờ mua), phân bổ trong mỗi tích giá $$ p\in (p_a,p_0)$$. Bản chất phía bên bid này là share của token USDC được đặt trong các khoảng giá $$ (1/p_0,1/p_a)$$ (do tính chất đối xứng của công thức xy=k) chờ để mua vào ETH. Nhưng do đặt trong cùng 1 hệ trục tọa độ với $$ Q_{ETH}(p)$$ nên ta phải quy về đơn vị share của ETH.

Như vậy xét về mặt toán học, ta có thể dễ dàng thấy tại bất kỳ điểm giá $$ p_0$$ nào ta cũng có công thức như sau:

$$$
\begin{cases}
x_0&=\displaystyle \int_{p_0}^{p_b}Q_{ETH}(p)dp \
y_0&=\displaystyle \int_{p_a}^{p_0}p*Q_{USDC}(p)dp
\end{cases}
$$$

Và tại điểm $$ p_0$$ là market price, như đã nói ở trên do AMM có spread = 0, giá bid và ask bằng nhau tại điểm này nên ta dễ dàng nhận thấy:

$$$
Q_{ETH}(p_0)=Q_{USDC}(p_0)=Q(p_0)
$$$

Theo CPMM, để làm tăng giá ETH từ $$ p_0 \rightarrow p_1$$ thì cần có 1 lệnh trade để lấy ra $$ -\Delta{x}$$ lượng ETH ra khỏi pool. Như vậy ta có:

$$$
\begin{align*}
\int_{p_0}^{p_1}Q_{ETH}(p)dp &=-\Delta{x} = -\Delta\left({\frac{L}{\sqrt{p}}} \right)
\end{align*}
$$$

Lấy đạo hàm 2 vế của phương trình trên, ta được:

$$$
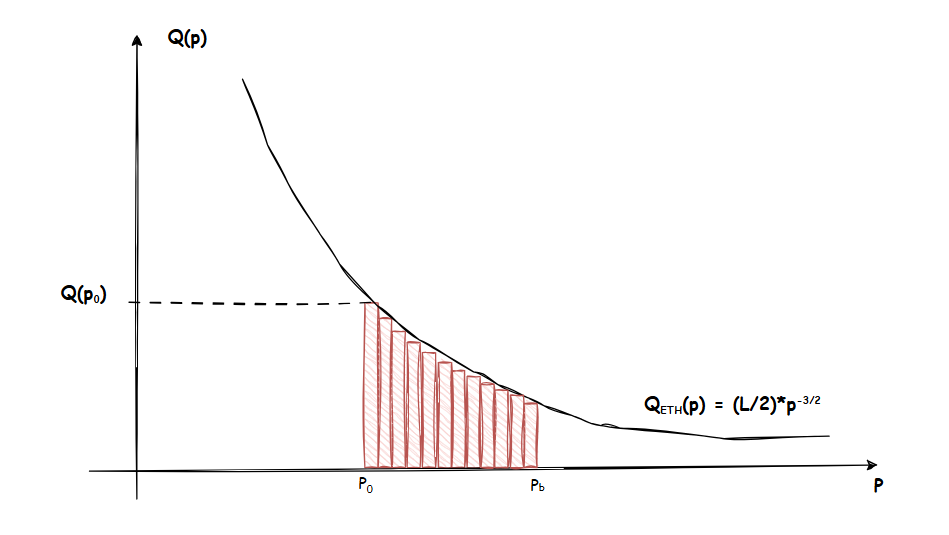
Q_{ETH}(p)=\left[ -\Delta\left({\frac{L}{\sqrt{p}}} \right)
\right]' = \dfrac{L}{2*\sqrt{p^3}}
$$$

Phân bổ liquidity của USDC

Do tính chất đối xứng của công thức $$ xy=L^2$$, ta có thể suy ra giá của USDC tính theo ETH là $$ u=\dfrac{1}{p}$$ , và share $$V_{USDC}(u)$$ của USDC (bản chất là số lượng token USDC trong hệ quy chiếu u) sẽ tuân theo công thức sau:

$$$
V_{USDC}(u)=\dfrac{L}{2*\sqrt{u^3}}
$$$

Do vậy, để convert từ $$ V_{USDC}(u)$$ trong hệ quy chiếu giá u về $$ Q_{USDC}(p)$$ hệ quy chiếu với giá p và đặt cạnh phân bổ liquidity $$ Q_{ETH}(p)$$ trên cùng 1 biểu đồ. Ta có phép chuyển như sau:

$$$
\begin{align*}
Q_{USDC}(p)&=uV_{USDC}(u)=u\dfrac{L}{2*\sqrt{u^3}} \
&=\dfrac{L}{2\sqrt{u}}=\dfrac{L\sqrt{p}}{2}
\end{align*}
$$$

Và khi biểu diễn phân bổ liquidity của ETH và USDC theo giá p, ta có hình giống “quả chuông úp ngược” (Bell-shape) như dưới đây:

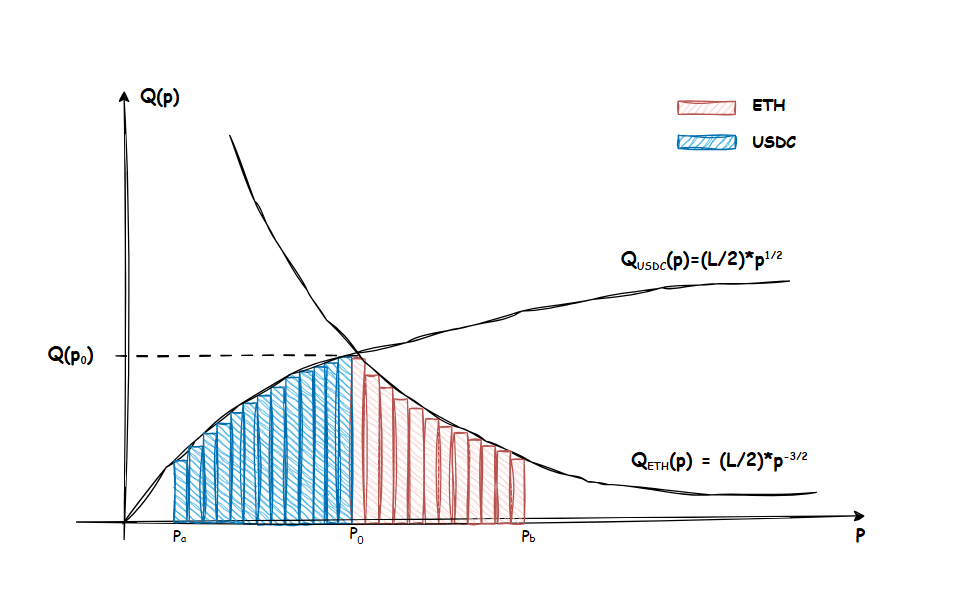
Một số kết luận thú vị

• Trái ngược với model V-shape của LOB trên các sàn CEX, phân bổ thanh khoản của Uniswap CPMM luôn tập trung đậm đặc ở giữa và mỏng dần về 2 phía giống dạng Bell-shape.

• Điều đó khiến cho mức spread = 0, MM không kiếm lợi nhuận từ spread mà bằng trading fees thu được khi giá giao dịch xung quanh market price $$ P_0$$

• Đó là 1 lợi thế của CPMM, nhưng cũng là nhược điểm vì tạo nên Impermanent Loss (IL) đáng kể gây nguy hại tới inventory của MM.

• Đối với model CLMM (Uniswap V3), khi $$ p \rightarrow p_a$$ thì $$ Q_{USDC}(p_a)=0$$ và toàn bộ liquidity trong pool chuyển thành ETH. Ngược lại, khi $ p \rightarrow p_b $ thì $$ Q_{ETH}(p_b)=0$$ và toàn bộ liquidity trong pool chuyển thành USDC. Hay nói cách khác, Uniswap V3 nén thanh khoản lại trong 1 khoảng hẹp $$ (p_a,p_b)$$ tạo nên capital efficiency lớn cho MM, nhưng đồng thời đẩy IL lên cực lớn.

• Đối với model CPMM (Uniswap V2), do p giao động trong khoảng $$ (0,\infty)$$ nên toàn bộ thanh khoản của ETH lẫn USDC sẽ được kéo giãn ra về vô cực khiến cho độ dốc của 2 đường đồ thị $$ Q_{ETH}(p)$$ và $$ Q_{USDC}(p)$$ gần như bằng 0. Điều đó khiến phân bổ thanh khoản của Uniswap V2 sẽ trở thành dạng đồng đều tại mọi điểm giá $$ p_0$$ và sẽ giống hình chữ nhật Rectangle-shape. Model này trung dung giữa Bell-shape của Uniswap V3 và V-shape. Nó cho IL trung bình, và trading fees thu được cũng ở mức trung bình.

• Tuy nhiên, Uniswap V2 được người “trong ngành” đánh giá là model DCA hoàn hảo nhất. Giá tăng lên thì sẽ giảm bớt ETH đi (bán dần ra), còn giá giảm xuống thì sẽ tăng dần ETH lên (mua dần vào). Ngoài ra, số lượng bán ra/mua vào vừa đủ để inventory 2 tài sản ETH và USDC luôn cân bằng nhau về tổng giá trị $$ px=y$$ là một phân bổ liquidity hài hòa khiến cho thanh khoản không bao giờ thiếu hụt, bất chấp việc price discovery có đi xa tới tận đâu đi chăng nữa.

• Qua việc nghiên cứu phân bổ liquidity của AMM ở trên, ta có thể dễ dàng rút ra playbook cho các cặp token khi tham gia LPing như sau:

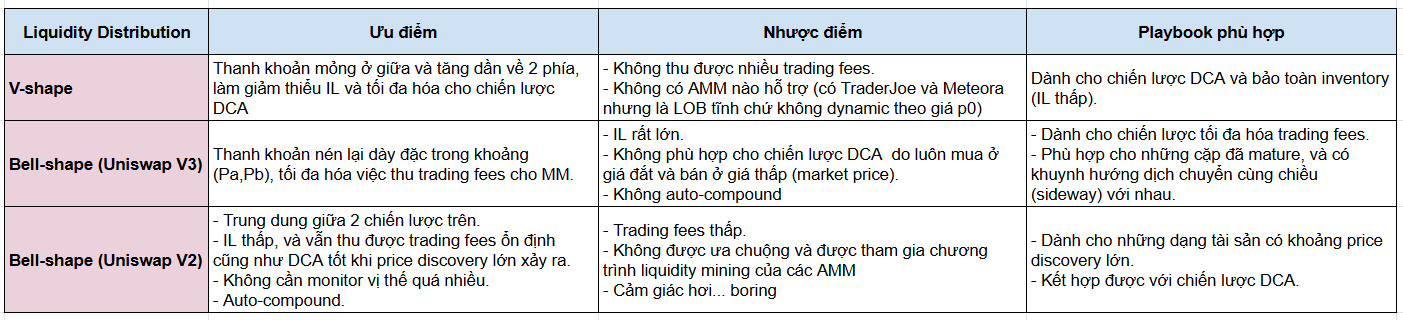
Episode này cũng khá dài, tôi xin kết thúc tại đây. Trong episode sau, tôi sẽ nối tiếp chủ đề này bằng cách phân tích model “elastic liquidity” của BrownFi , một dạng AMM hoạt động dựa vào Oracle để có thể tập trung/kéo dãn thanh khoản phù hợp với size của từng lệnh trade, qua đó có thể tận dụng lợi thế của cả 2 model Uniswap V2 và Uniswap V3 kể trên.

* Bài viết này dựa trên nghiên cứu của bạn Tuấn Trần (Co-founder BrownFi) cùng các cộng sự, được đăng tải trên tạp chí IEEE. Bạn có thể đọc toàn bộ nghiên cứu đó tại ĐÂY