"Cryptography is serious, with ideas often hard to understand. When we try to explain them with cartoons and cute narratives, I don’t think we make our contributions easier to understand. What we actually do is add in a layer of obfuscation that must be peeled away to understand what has actually been done."

P. Rogaway, the paper “The Moral Character of Cryptographic Work”

Disclaimer: this write up mostly relies on the legendary Dan Boneh’s course “Cryptography I”. If you have time – watch the course. Otherwise, continue reading.

TL;DR

This article explores basics of ciphers, discovering and explaining its ingredients to provide the reader with some understanding of the topic in a structured way. It first gives a bunch of definitions to ensure we’re on the same page. Then it defines what is a cipher, where we can see them in blockchain and what are the core cipher types. The next section provides some intuition of how to think about cipher security. Finally, it tells a bit about the most popular attacks. The icing on the cake – the key exchange protocols that are an essential component of almost any cipher bur are considered a black box up to the last section.

Introduction

Even though we usually speak about cryptography in the blockchain context, the cryptography started outside blockchain and is currently everywhere: securing communication (e.g., encrypting web traffic, wifi connection, cell phone, bluetooth, etc.), encrypting files on disk, protecting contents (e.g., DVD or Blu-ray), user authentication (e.g., elections and auctions), and many more.

Cryptography is a tremendous tool but it is not a solution for all security problems.

For example, cryptography does not secure us from software bugs or social engineering attacks. Correct implementation is a part of cryptography security: that is, even if the cryptographic construction is absolutely secure the improper implementation can easily break the security.

Contents

In this article, we will mostly talk about secure communication case and will cover both establishing shared secret key and data transmission.

• Introduction

• Definitions

• What is a cipher

• Ciphers in blockchain

• Types of ciphers

  • 1. One Time Pad (OTP) Cipher

  • 2. Stream Cipher – a modification of OTP

  • 3. Block Cipher

  • PRP examples

    • DES

    • 3DES

    • AES

  • Using Block Ciphers

    • CBC (Cipher Blockchaining Mode)

    • CTR (the Counter Mode)

  • Cipher security

  • 4. MAC ciphers

• Keys: one-time keys vs many-time keys

• Types of attacks

• Key Exchange

• Data Encryption Standard and conclusions

• Sources

Definitions

Disclaimer: the definition list quit long, however, there is no need to read it all. Just check that the listed words are familiar to you so it will be easy to understand the main part of the article. If some word sounds a bit vague – check the explanation =)

• Message – a piece of data one party is sending to another party.

• Plaintext – unencrypted message readable for a human. Message and plaintext can be considered to mean the same thing.

• Ciphertext – message encryption performed on plaintext using an algorithm, called a cipher.

• Least significant bit (LSB) – the rightmost bit in a binary number representation.

• Most significant bit (MSB) – the leftmost bit in a binary number representation.

• Block – fixed-length group of bits.

• Adversary – a malicious entity whose aim is to prevent the users of the cryptosystem from achieving their goal (primarily privacy, integrity, and availability of data).

• Active Adversary – a much more highly skilled cyber criminal, possibly with sophisticated software and networking skills, who will gain entry to the systems, possibly lay dormant for a period of time, and wait for opportunities to target code or execute scripts that prevent themselves from being detected while they look for and exfiltrate higher value data and assets. In our case, we assume an adversary to be active if their goal is message modification (tampering) not just eavesdropping.

• Symmetric encryption – two parties share the same secret key $$k$$, and there are two algorithms: encryption algorithm $$E$$ and decryption algorithm $$D$$. $$E$$ takes as inputs the message $$m$$ and the key $$k$$ and produces a cipher $$c: E(m,k) = c$$. $$D$$ takes as inputs the cipher $$c$$ and the key $$k$$ and decrypts the message $$m: D(c,k) = m$$. The algorithms $$E$$ and $$D$$ are publicly known.

• Asymmetric encryption (public key encryption) – uses pairs of related keys. Each key pair consists of a public key and a corresponding private key. Key pairs are generated with cryptographic algorithms based on mathematical problems termed one-way functions.

• Secret key (private key) – in symmetric cryptography, a piece of information, usually a string of numbers or letters, which, when processed through a cryptographic algorithm, can encode or decode cryptographic data.

• Public key – used to encrypt data securely before it is sent over the internet.

• One-way function – a function that is easy to compute on every input, but hard to invert given the image of a random input.

• Key space – the set of all valid, possible, distinct keys of a given cryptosystem.

• Confidentiality – the attacker can’t know anything about what messages are communicated.

• Integrity – ensuring that information remains unaltered and free from tampering.

• Alice and Bob (sometimes Alice, Bob, and Eve) – fictional characters commonly used as placeholders in discussions about cryptographic systems and protocols, and in other science and engineering literature where there are several participants in a thought experiment.

• Deterministic algorithm – an algorithm that, given a particular input, will always produce the same output.

• Randomized algorithm – an algorithm that employs a degree of randomness as part of its logic or procedure.

• Efficient algorithm – the algorithm runs within the polynomial time.

• $$XOR$$ – mod 2 addition. For the goals of this article, we should keep in mind that (i) $$a ⊕ b = b ⊕ a$$, (ii) $$x ⊕ x = 0$$, (iii) $$x ⊕ 0 = x$$.

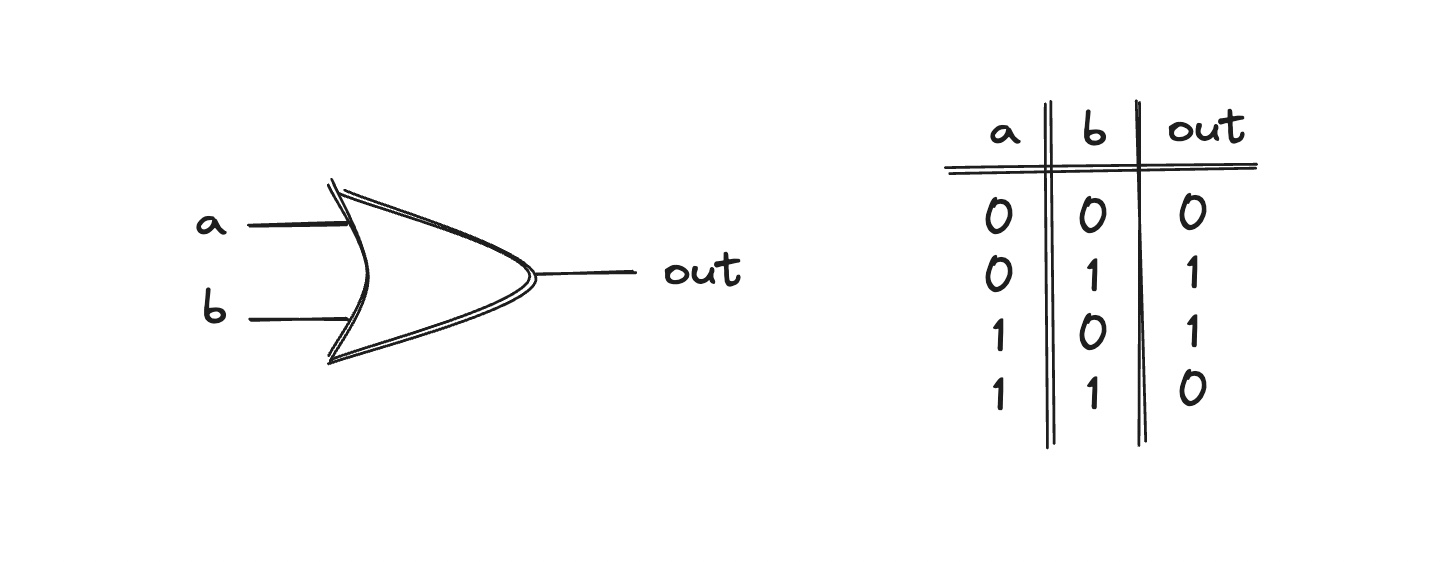
• Permutation – rearrangement of elements.

• Padding – adding data to the beginning, middle, or end of a message prior to encryption. It can be used to prevent an attacker from knowing the exact length of the plaintext message, to achieve a specific required message length, etc.

• Dummy block – a block which contains only padding bytes. It can be used as a signal for decryptor of how many padded bytes should be removed.

• Negligible and non-negligible probability – while talking about ciphers’ security, we often refer to negligible and non-negligible probability. Negligible can be informally explained as a very very small. However, there is no specific universal number of what is very very small. It depends on the one who defines and the specific case.
  In practice, we say that the scalar ε is negligible if $$ε ≤ 2^n$$, where $$n$$ can be 30 or 80 or other number. By “depending on the case”, we mean that something (like collision) shouldn’t happen over the key life for a specific cipher.

• Nonce – a unique value that doesn’t repeat during the whole key life. Note, there is no requirement for nonce to be random.

• Probability distribution – the probabilities of occurrence of different possible outcomes.

• Uniform probability distribution – every possible outcome has an equal likelihood of happening.

• Theorem: if $$Y$$ is a random variable arbitrary distributed (i.e. we know nothing about its distribution) over $${0,1}^n$$ and $$X$$ is an independent (from $$Y$$) random variable uniformly distributed over $${0,1}^n$$ then $$z = x ⊕ y$$ is a uniformly distributed random variable over $${0,1}^n$$. This $$XOR$$ property low-key explains why cryptographers like using $$XOR$$.

• The birthday paradox: let $$r_1,…,r_n∈U$$ be independent identically distributed random variables, then when $$n = 1.2 * U^{1/2}$$, $$Pr[∃i≠j: r_i = r_j] ≥ 1/2$$. That is, if one samples $$1.2 * U^{1/2}$$ variables from the set, the probability that two of them will be the same is larger than $$1/2$$.

That was a bunch of definition that are good to know to move further to meet ciphers!

What is a cipher

A cipher, defined over $$(K, M, C)$$ where $$K$$ is the set of all possible keys, $$M$$ is the set of all possible messages, and $$C$$ is the set of all possible ciphers, is a pair of “efficient” algorithms $$E$$ and $$D$$, where $$E: K × M → C$$ and $$D: K × C → M$$ such that $$∀m ∈ M$$ and $$∀k ∈ K: D(k, E(k,m)) = m$$.

Ciphers in blockchain

As we told in the introduction – cryptography is everywhere and ciphers are everywhere. For a more specific example, we should mention hash functions (e.g. SHA256) and digital signatures (e.g. ECDSA) that deal exactly with ciphers. Furthermore, new specific ciphers are constructed on a regular basis to be more efficient or provide specific properties. For example, a while ago the Poseidon hash function was suggested as a zk-specific one.

Types of ciphers

Note: ⊕ is a notation for XOR.

1. One Time Pad (OTP) Cipher

• $$M = C = K = {0,1}^n$$, that is, the message, the cipher, and the key are a string of the same n-bit length.

• $$c = E(k,m) = k ⊕ m$$.

• $$m = D(k,c) = k ⊕ c$$.

• To prove that the One Time Pad Cipher is consistent, check if $$D(k, E(k,m)) = m$$. $$D(k, E(k,m)) = D(k, k ⊕ m) = k ⊕ (k ⊕ m) = (k ⊕ k) ⊕ m = 0 ⊕ m = m$$. So, the OTP cipher is consistent.

• The advantage of OTP is that encryption and decryption are really fast. The disadvantage is that the ciphertext is as long as the plaintext.

2. Stream Cipher – a modification of OTP

• Uses a pseudorandom key instead of a random key.

• A pseudorandom generator (PRG) is a function $$G: {0,1}^s → {0,1}^n$$ with $$n >> s$$. That is, the function $$G$$ maps an s-bit string (a seed space) into an n-bit string (an output) where n is much much larger than s and an output looks random. PRG can also include a nonce.

  Using PRG, one can have a small key $$k$$, but using the algorithm $$G$$, $$G(k)$$ will be of the same length as the message:

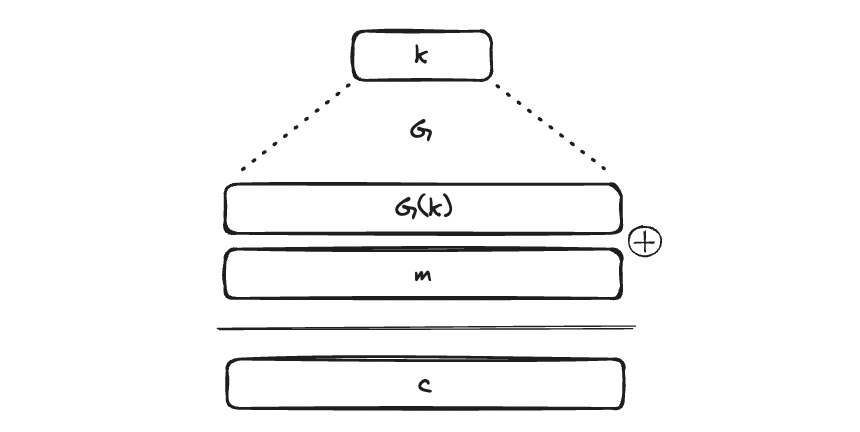
• The function $$G$$ should be deterministic, efficient and unpredictable. By unpredictable, one means that given the first i bits of $$G(k)$$, it is impossible to predict any single other bit of $$G(k)$$.

  Stream Cipher security directly depends on the PRG security. For PRG to be secure, the distribution of its outputs should be indistinguishable from the uniform distribution. In other words, it means that the PRG output looks random.

Going back to the Stream Cipher:

• $$c = E(G(k),m) = G(k) ⊕ m$$.

• $$m = D(G(k),c) = G(k) ⊕ c$$.

• A modern example of a Stream Cipher is Salsa 20: $${0,1}^{128/ 256} × {0,1}^{64} → {0,1}^n$$ where $${0,1}^{128/ 256}$$ is the seed, $${0,1}^{64}$$ is the nonce, and $${0,1}^n$$ is the ciphertext. Salsa 20 takes two inputs: the key $$k$$ and the nonce r and adds counter. $$Salsa \ 20 = H(k, (r,0)) || H(k, (r,1)) || …$$ where $$H$$ can be described as following:

$$h$$ is an invertible function, and 𝜏 are some pre-defined constants.

3. Block Cipher

• A pair of algorithms $$(E, D)$$ that take an n-bit input and produce an n-bit output using a k-bit key $$k: E(k,m) = c$$, $$D(k,c)=m$$.

• Block cipher works by iteration. In particular, it takes key $$k$$ as an input and expands it into $$n$$ keys. Then it iteratively uses the round function $$R(m_{n-1},k) = m_n$$.

To understand the construction of block cipher, we need to introduce PRF and PRP – Pseudo Random Function and Pseudo Random Permutation

• Pseudo Random Function (PRF) defined over $$(K,X,Y)$$ where $$K$$ is the key set, $$X$$ is the input set, and $$Y$$ is the output set, is the function $$F: K×X→Y$$ such that there exists an efficient algorithm to evaluate $$F(k,x)$$.

  PRF can be used to construct PRG. For example, $$G(k) = F(k,0) || F(k,1) || … || F(k,t)$$.

• Pseudo Random Permutation (PRP) defined over $$(K,X)$$ where $$K$$ is the key set, and $$X$$ is the input and output set is the function $$E: K×X→X$$ such that (i) there exists an efficient deterministic algorithm to evaluate $$E(k,x)$$, (ii) the function $$E(k,⋅)$$ is one-to-one, and (iii) there exists an efficient inversion algorithm $$D(k,y)$$.

  Formally, PRP is a PRF where $$X = Y$$ and the function is efficiently invertible. And any secure PRP is a secure PRF whenever the set $$X$$ is sufficiently large.

PRP examples

A couple of pretty widely known modern examples of PRPs are 3DES and AES.

To describe 3DES, let’s first take a look at DES – the ancestor of the two PRPs mentioned above.

DES: The Data Encryption Standard

• The DES basis is the Fesitel Network that takes $$d$$ arbitrary functions $$f_1,…,f_d: {0,1}^n → {0,1}^n$$ and constructs an invertible function $$F: {0,1}^{2n} → {0,1}^{2n}$$.

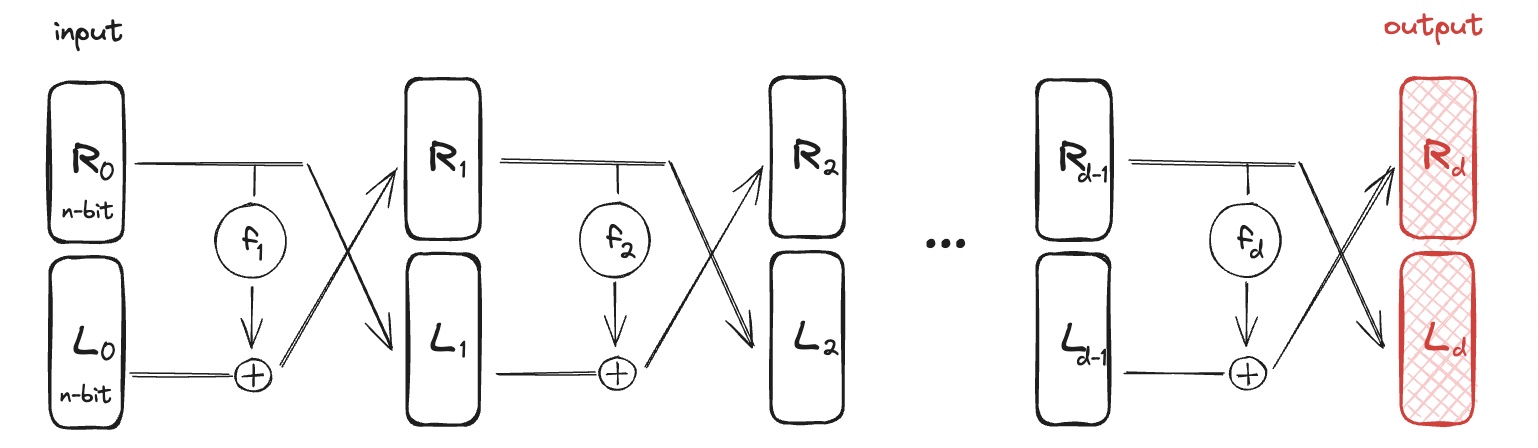
If $$f: K×{0,1}^n→{0,1}^n$$ is a secure PRF, then 3-round (with 3 different independent keys) Feistel $$F: K^3×{0,1}^{2n}→{0,1}^{2n}$$ is a secure PRP.

• DES is 16-round Feistel Network constructed with 16 arbitrary functions $$f_1,…,f_{16}$$ and 16 different independent keys (that are expanded from the initial key k):

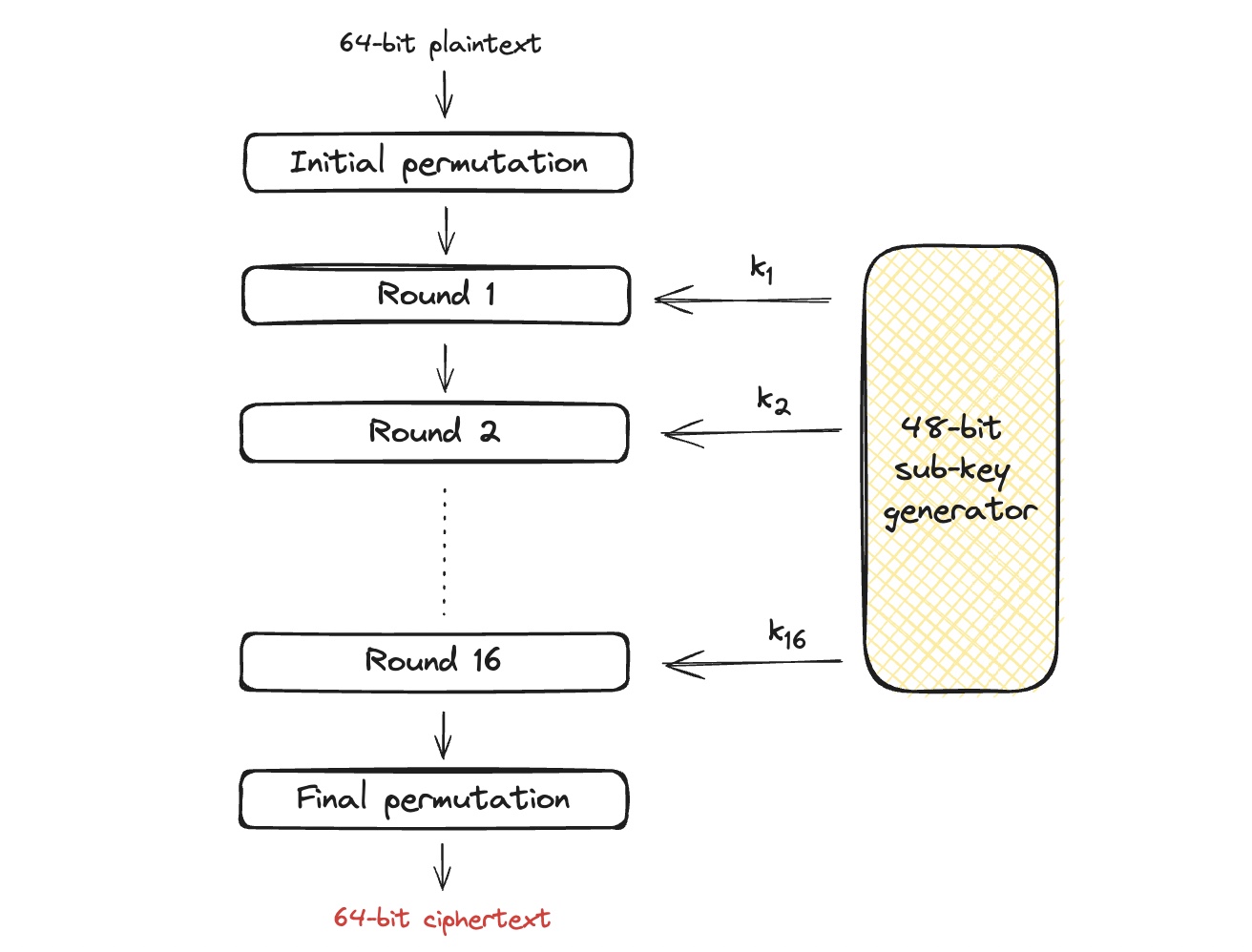
To specify what is a round:

• Where $$E$$ is an expansion functions that maps 32-bit input into 48-bit output replicating and permutating the bits.

• $$P$$ is the permutation functions that maps 32-bit input into 32-bit output.

• $$s_i$$ is a function in a form of lookup table that maps 6-bit input into 8-bit output.

3DES

However, DES was easy to break by exhaustive search. In 1998, DES was broken by the “deep crack” Machine built by the Electronic Frontier Foundation (EFF) that cost $250k. In 2006, it was broken by 120 FPGAs that cost $10k. The core problem was 56-bit key that is too small in terms of the key set size – $$2^{56}$$.

To strengthen DES construction from the exhaustive search attack, the 3DES (the Triple Data Encryption Standard) was introduced. In 3DES the key length is 56*3=168 bits. So the key set contains $$2^{168}$$ elements that is already can’t be broken by the exhaustive search attack (at least today).

• Let $$E: K×M→M$$ be a block cipher.

• $$3E: K^3 × M → M$$ as $$3E((k_1,k_2, k_3),m) = E(k_1, D(k_2, E(k_3,m)))$$.

• 3DES is 3 times slower than DES.

• 3DES is a NIST standard.

AES (The Advanced Encryption Standard)

• For modern hardware, 3DES was too slow, so the AES algorithm was introduced. It was adopted as a standard in 2000, has 128-bit block size and the key size can be 128-bit, 192-bit, or 256-bit long. The larger the key – the more secure the cipher, but at the same time the larger the key – the slower the cipher.

• AES is based on the Substitution-Permutation Network:

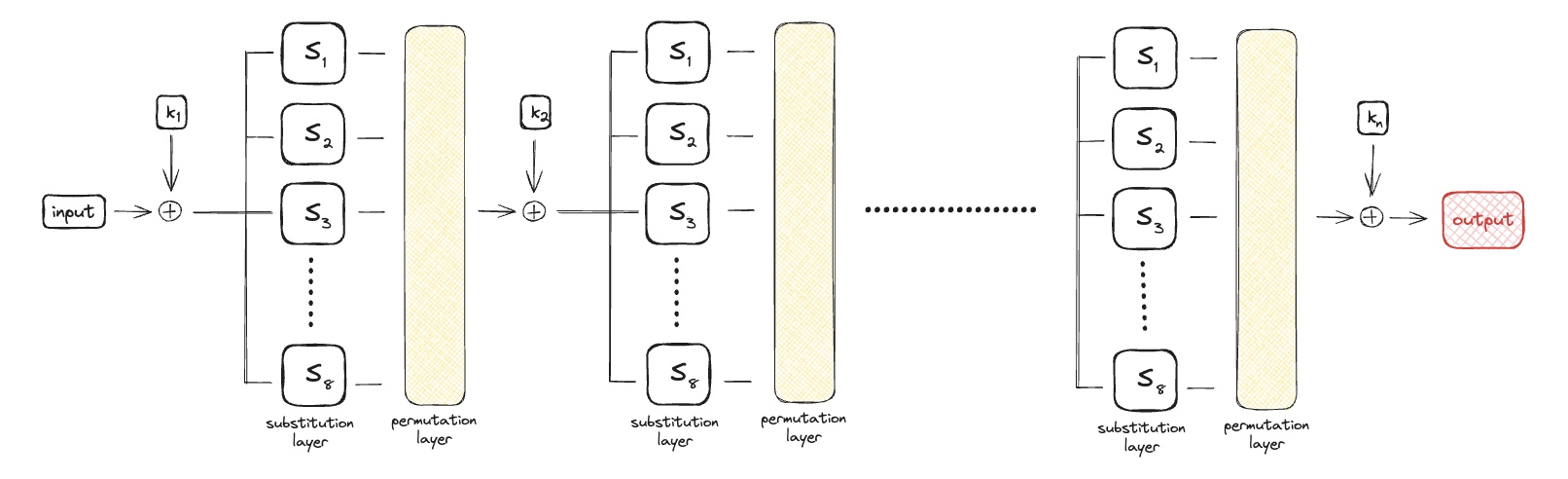
The substitution and permutation layers include

• ByteSub() function that is a 1-byte S-box (a 256-byte lookup table) applied to each byte of the input;

• ShiftRow() function cyclically shifts the rows (cyclically means that the first row is shifted by one position, the second row is shifted by two positions, etc.);

• MixColumn() function that applies a linear transformation to each column;

• AddRoundKey() function is used to map an initial 16-bit key into 11 keys $$k_0,…,k_{10}$$, 16-bit long each.

Using Block Ciphers

Block cipher mode is an algorithm that uses a block cipher to provide information security such as confidentiality or authenticity.

Two widely-known cipher modes are CBC (Cipher Blockchaining Mode) and CTR (the Counter Mode). Below we are exploring them in more details.

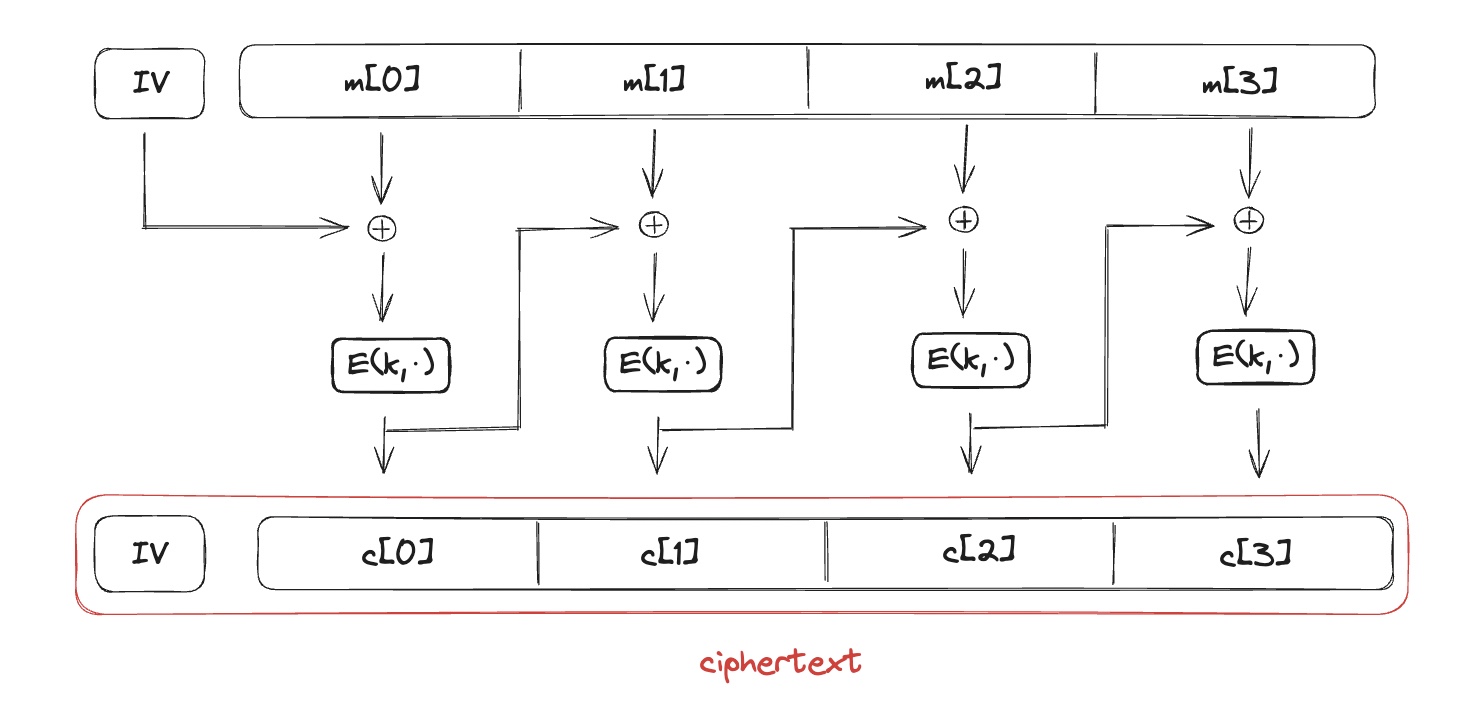
CBC (Cipher Blockchaining Mode)

• Let $$IV$$ be unpredictable and randomly chosen from $$X$$ and $$(E,D)$$ be a PRP.

CTR (the Counter Mode)

Let $$F$$ be a secure PRF, $$F: K×{0,1}^n → {0,1}^n$$.

The CTR works as following:

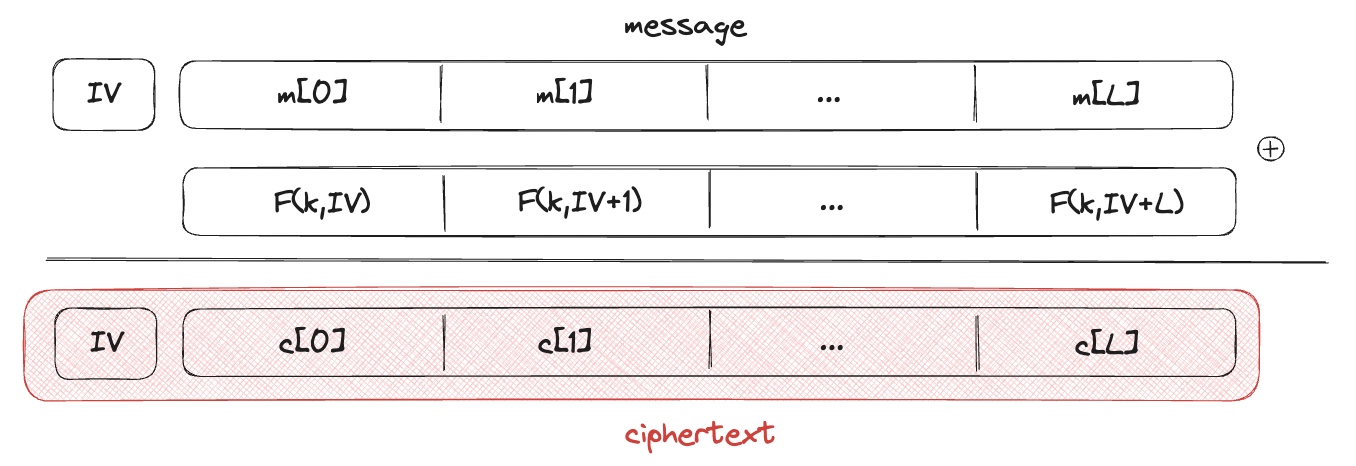
Note: unlike CBC, CTR is parallelizable that allows to accelerate the encryption if having several hardware machines.

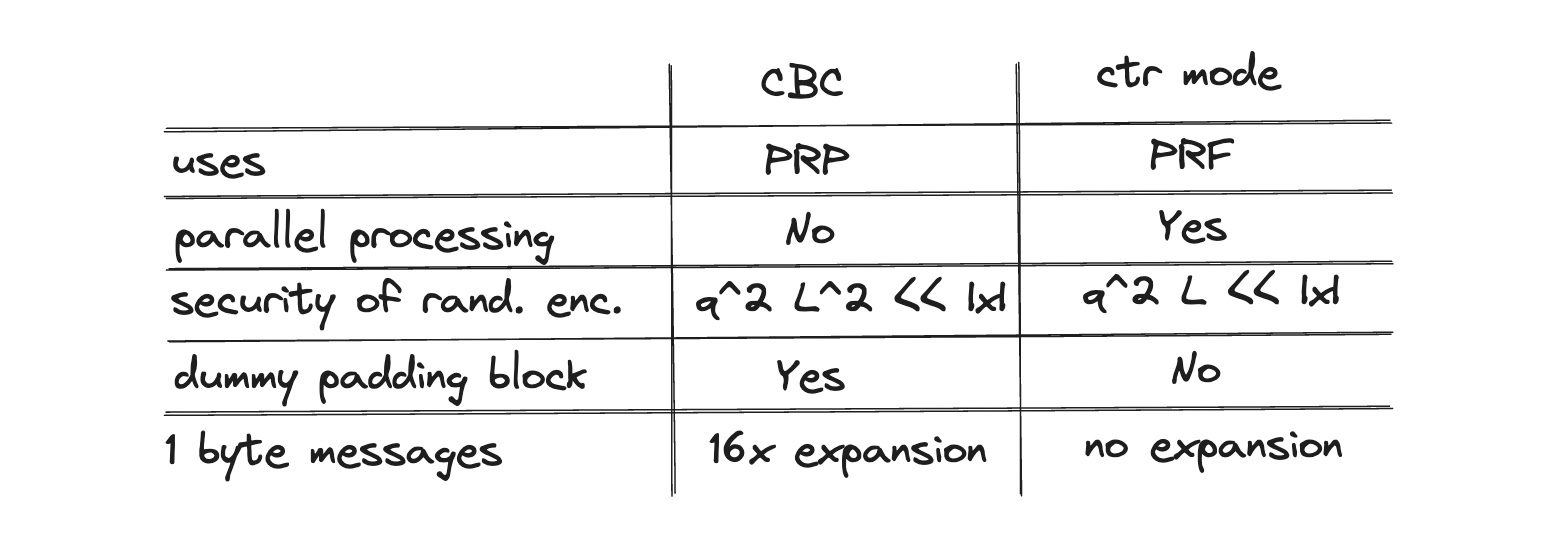
In modern world, CTR is more popular and widely-adopted than CBC because it is superior over CBC by all criteria:

Keys: one-time keys vs many-time keys

One-time key is used only once to encrypt only one message. Hence, the adversary sees only one ciphertext encrypted with a particular key.

When we use the key many times (many-time key) – the adversary sees many ciphertexts encrypted with the same key. That if used in a trivial way might lead to some attacks such as chosen plaintext attack (check the section “Types of Attacks” to learn more.)

There are several ways to mitigate the risk of many-time key exploit:

1. Randomized ecnrytption: encrypting the same message twice will give different results thanks to adding some random bits. In this case, the ciphertext will be larger than the plaintext.

2. Nonce-based encryption: instead of taking two inputs $$k$$ and $$m$$ such that $$c = E(k,m)$$ the encryption algorithm now takes three inputs, $$k$$, $$m$$, and $$n$$, where $$n$$ is the nonce, such that $$c = E(k,m,n)$$ and the pair of $$(k,n)$$ never repeats.

   Nonce can be used as a counter (0, 1, 2, 3, …), then there is no need to provide nonce for decryption, as both parties (encrypting and decrypting) can have the same counter.

   As another approach – nonce can be randomly picked from a nonce set though then the set should be large enough so that the nonce won’t repeat within the key life.

One should mention that even though the many-time key can be used many times it doesn’t mean infinitely many times. Depending on specific security assumptions, the many-time key still should be changed. For example, in AES, the key should be changed after each $$2^{48}$$ blocks and in 3DES after each $$2^{16}$$ blocks.

Cipher security

Disclaimer: One might say that security consists of confidentiality (the ciphertext does NOT disclose anything about the plaintext) and integrity (NO data modification is possible). However, there are use cases when only of them is necessary. So, there can be different ciphers that provide only confidentiality or only integrity or both of them.

Confidentiality

1. Perfect secrecy: the ciphertext reveals no information about the plaintext, in other words, no eavesdropping is possible. Formally, a cipher(E,D) has perfect secrecy if $$∀m_0,m_1∈M$$ that the attacker can really exhibit explicitly such that $$len(m_0)=len(m_1)$$ and $$∀c∈C$$, $$Pr[E(k,m_0)=c] ≈ Pr[E(k,m_1)=c]$$ where k is uniformly distributed over K and ≈ stands for “computationally indistinguishable”. To calculate this probability, for any given message $$m∈M$$ and cipher $$c∈C$$, the probability that m is mapped into c is number of $$k∈K$$ such that $$E(k,m) = c$$ divided by total number of $$k∈K$$.

2. Semantic Security: there are two parties, a challenger and an adversary. The adversary sends the challenger two messages, $$m_0$$ and $$m_1$$. The challenger encrypts one of them and sends it back to the adversary. The adversary is expected to tell which of the messages was encrypted.

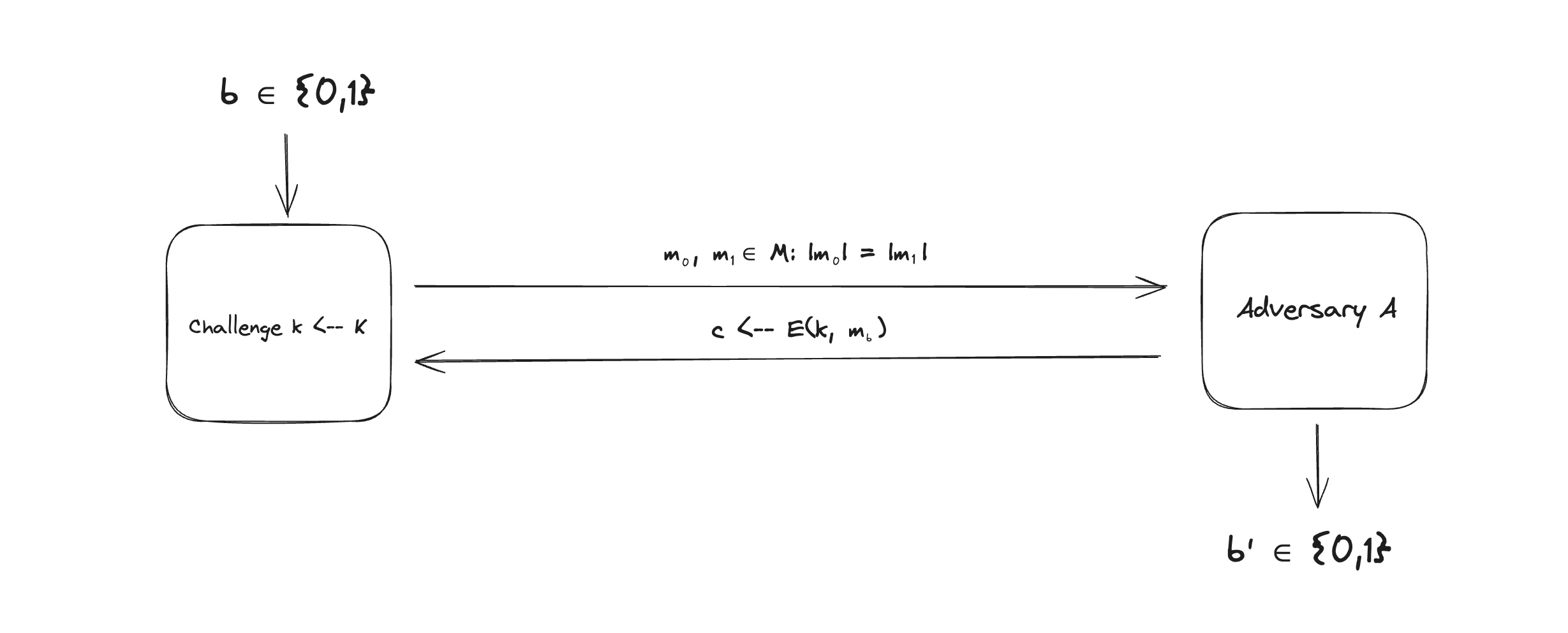
for $$b = 0, 1: W_b := [event \ that \ EXP(b) = 1]$$

If an adversary cannot guess with better probability than $$1/2$$, then we say that the cipher is semantically secure.

To clarify the difference between perfect secrecy and semantic security, perfect secrecy implies that the cipher text is impossible to break, whereas semantic security implies that cipher text is infeasible to break with high probability.

Integrity

To provide message integrity, one uses MAC – Message Authentication Code consisting of two algorithms $$(S,V)$$ where $$S$$ is the signing algorithm and $$V$$ is the verification algorithm.

Note: MAC provides only integrity without confidentiality.

• The sender generates a tag: algorithm $$S$$ takes message $$m$$ and key $$k$$ as inputs and produces a ‘short’ tag: $$tag ← S(k,m)$$;

• The sender sends the message and the tag to the second party;

• The second party applies the tag verification algorithm to check that the message wasn’t tempered: $$V(k,m,tag) =$$ “yes” or “no”.

Secure MAC means that the attacker (i) can’t produce a valid tag for a new message, (ii) given a pair of a message and a tag $$(m,t)$$, the attacker can’t produce a pair $$(m,t’)$$ for $$t ≠ t’$$.

Collision Resistance

• Let $$H$$ be a hash function $$H: M→T$$ where $$|M| >>|T|$$.

• A collision for $$H$$ is a pair $$m_0, m_1 ∈ M$$ such that $$H(m_0)=H(m_1)$$ and $$m_0≠m_1$$.

• A function is collision resistant if it is “hard to find” collisions for this function.

4. MAC ciphers

MAC provides integrity only (no confidentiality).

• A secure MAC can be constructed using secure PRF, then the signing algorithm $$S(k,m) = F(k,m)$$. Hence, AES is a MAC for 16-byte messages.

• For “arbitrary” large messages, CBC-MAC (often used in banking system for provide integrity for account transfers) and HMAC (often used in internet protocols such as SSL) are the most widely-used. In particular, they convert small PRF into large PRF and then use it to construct MAC.

Encrypted CBC-MAC (ECBC) – consequent construction

• Let $$F$$ be a PRP, $$F: K×X→X$$;

The ECBC works as following

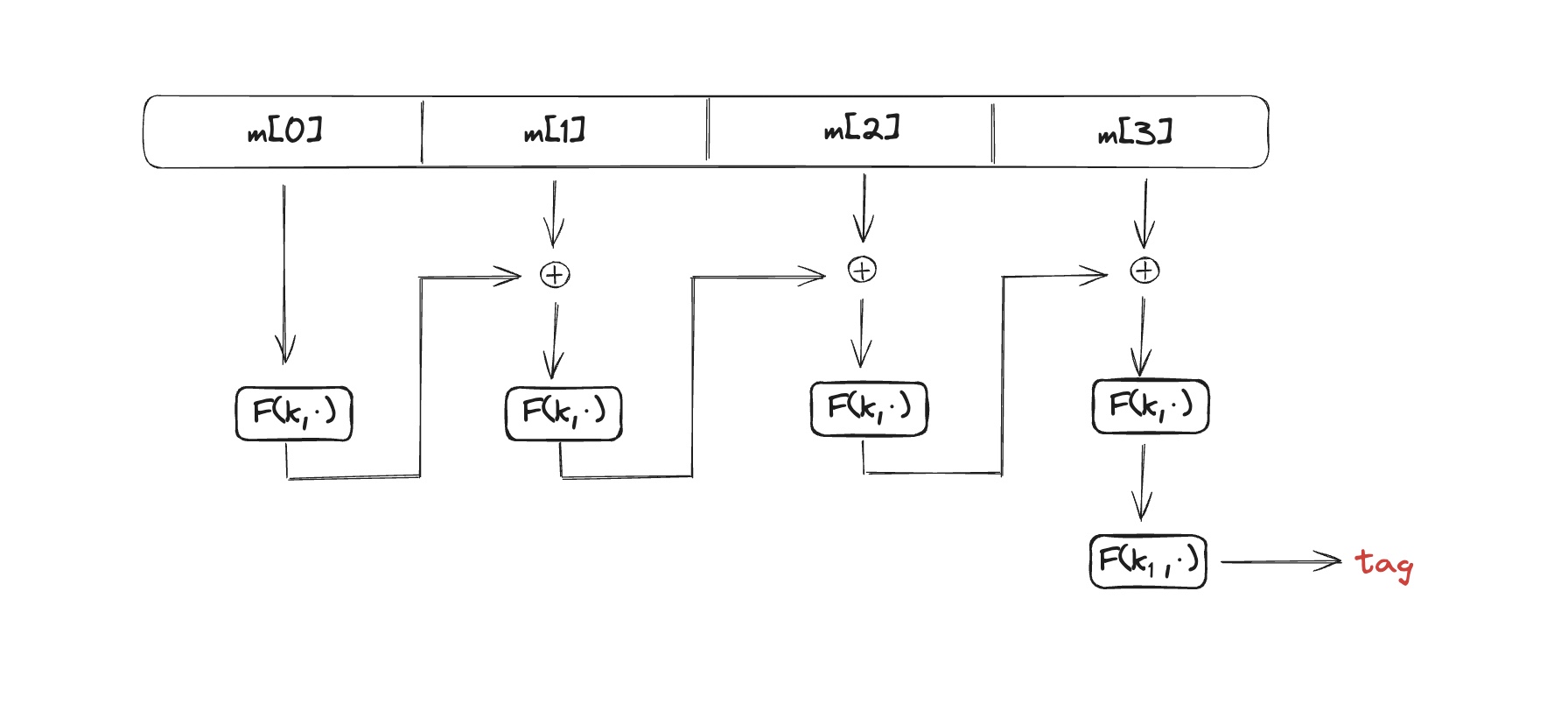
where a new PRF takes a pair of keys $$(k, k_1)$$ and an arbitrary long message $$X$$. It then splits this message into blocks of equal size $$m[0], m[1], …,$$ apply function $$F$$ consequently to each block, XORing the result of the step $$n-1$$ with $$m[n]$$ and using it as an input to a new iteration of function $$F$$.

PMAC – parallel construction

• Let $$F$$ be a PRP, $$F: K×X→X$$;

The PMAC works as following

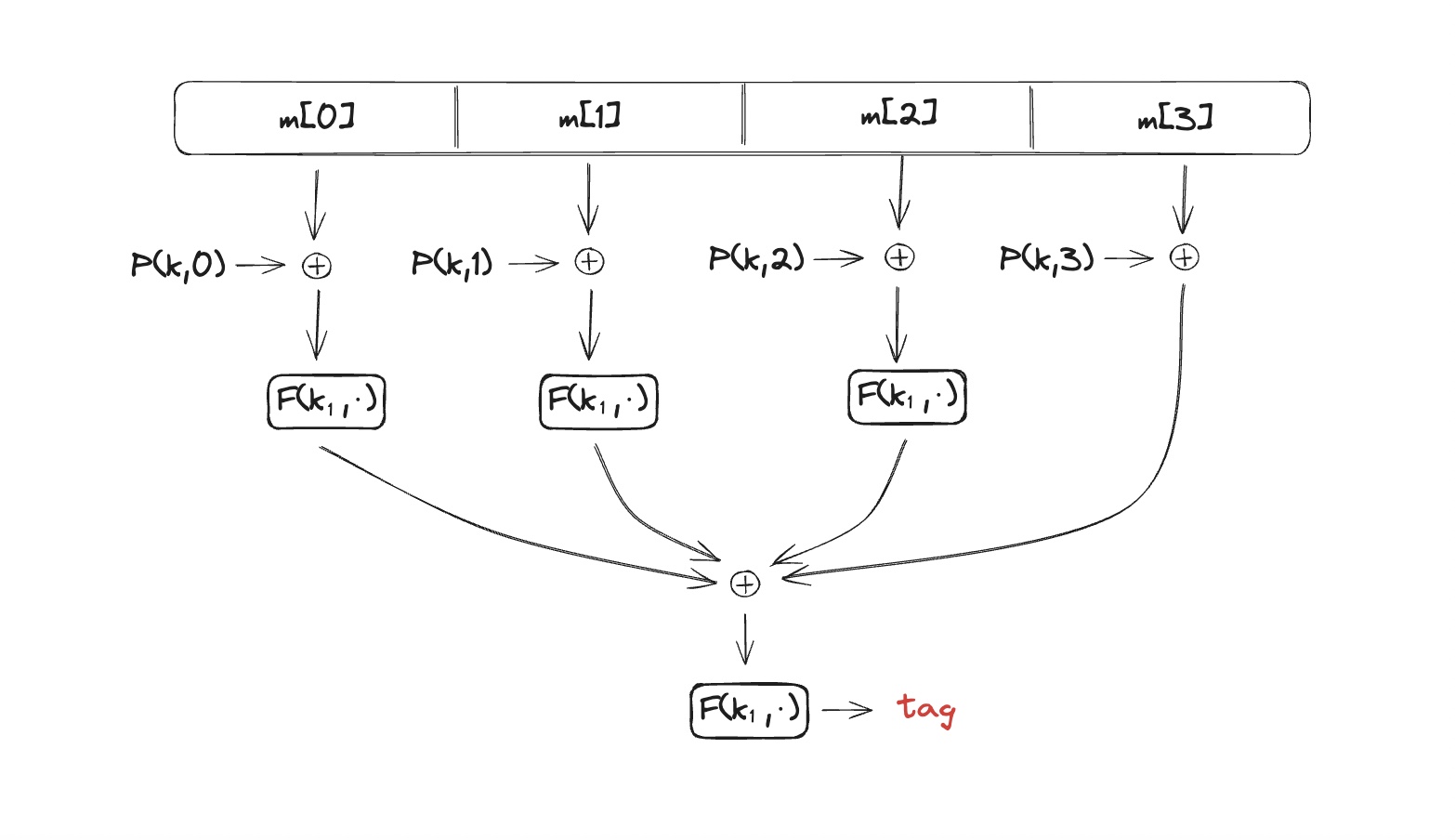
where function P enforces a specific block order preventing from malicious block swap.

Hash-MAC (HMAC)

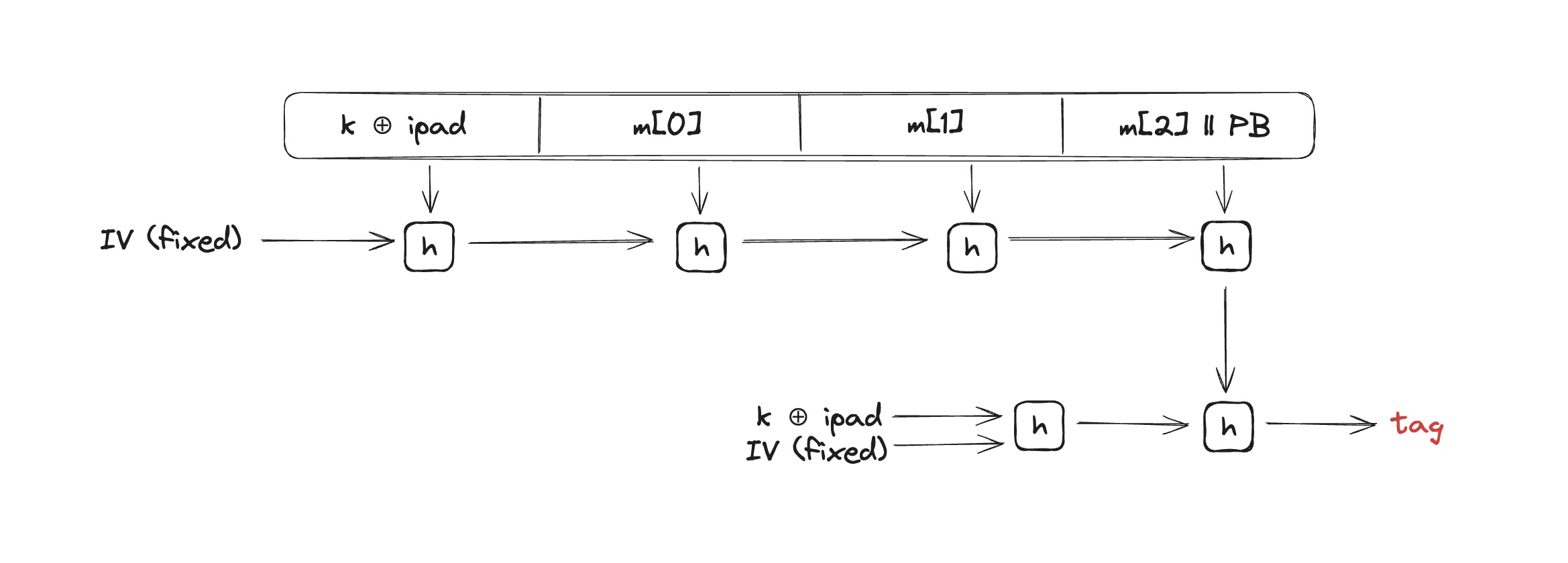
where ipad is internal pad.

Confidentiality AND integrity

If one needs both properties – authenticated encryption is used.

An authenticated encryption system $$(E,D)$$ is a cipher where $$E: K × M × N → C$$ and $$D: K × C × N → M ∪ {⊥}$$ where ⊥ means that the ciphertext is rejected and $$⊥∉ M$$.

Types of attacks

Disclaimer: the list is not exhaustive.

• Ciphertext only attack – the attacker has access only to the ciphertext and attempts to derive the plaintext or the encryption key without any knowledge of the encryption algorithm or the key used.

• Two Time Pad attack – for OTP and Stream Cipher, if one uses the same key twice: $$c_1 = G(k) ⊕ m_1$$ and $$c_2 = G(k) ⊕ m_2$$. The adversary can decrypt the messages $$m_1$$ and $$m_2$$ by XORing $$(G(k) ⊕ m_1) ⊕ (G(k) ⊕ m_2) = m_1 ⊕ m_2$$. To mitigate the issue, one can use nonce.

• Related Key Attack – the attacker has access to pairs of plaintexts and their corresponding ciphertexts that are encrypted with different keys that are related in some way. This attack exploits the relationship between the keys to uncover.

• Exhaustive search attack (brute force attack) – trying every possible key until the correct key is identified.

• Meet-in-the-middle attack (MITM) – exploits the relationship between two halves of the encryption process to reduce the computational complexity required to find the secret key. The attack involves encrypting plaintext with one key and decrypting ciphertext with another key simultaneously, essentially meeting in the middle of the encryption/decryption process.

• Timing attack – a type of side-channel attack that exploits the variations in the time it takes for a system to perform cryptographic operations.

• Power attack – a type of side-channel attack that exploits the variations in the power consumption of a device while it performs cryptographic operations.

• Side channel attack – precise measurement of time to encrypt and decrypt and consumed power for encryption and decryption.

• Fault attack – causing the smartcard to malefunction at the right moment might expose the secret key.

• Chosen Plaintext Attack (CPA) – under security check, instead of providing two different messages m_0 and m_1, the adversary provides two same messages m and m, and a result it gets c = E(k,m). So, with a many-time key, the adversary can get arbitrary many pairs (m,c) encrypted with the same key and break the cipher, that is to produce a valid new message.

• Chosen Ciphertext Attack (CCA) – the attacker can choose arbitrary ciphertexts and obtain their corresponding plaintexts, typically through an oracle. The goal of this attack is to exploit the decryption process to reveal information about the secret key or to decrypt other ciphertexts.

• Verification timing attack – a specific type of side-channel attack that exploits the time variations in the execution of cryptographic operations, particularly during the authentication or verification processes.

• Collision attack – the goal is to find two distinct inputs that produce the same hash output.

• Replay attack – an attacker intercepts and captures a valid data transmission, such as a message or transaction, and then maliciously retransmits that data to deceive the system into thinking it is a legitimate request.

• Side channel attack – gaining information from the physical implementation of a computer system.

• Padding attack – exploits the way data is padded before encryption.

• Dictionary attack – systematically entering every word in a predefined list (dictionary) of likely passwords.

Key Exchange

In most data exchange cases we mention above it is assumed that two parties have a shared secret key. How can they do it:

• Option 1 (the most obvious one): online trusted third party (TTP) creates a shared key and shares it with both partied: for (toy) example, party $$A$$ has a key $$k_A$$, party B has a key $$k_B$$, the trusted third party creates a key $$k_{AB}$$. It encrypts the shared key using $$k_A$$ and sends to the party $$A$$ and also encrypts using $$k_B$$ and sends to the party $$B$$.

However, the trusted third party introduces trust that is an undesirable property for a robust system. Can we do better?

• Option 2: Merkle Puzzles

  • Alice prepares $$2^{32}$$ puzzles.

  • Bob picks one random puzzle and solves it by brute-forcing (checking all possible $$2^{32}$$ values). As a result, Bob obtains $$(x_i, k_i)$$ and sends $$x_i$$ to Alice so she knows Bob has solved the puzzle. $$k_i$$ is now used as a shared key between Bob and Alice.

• Option 3: the Diffie-Hellman protocol

Fix a large prime $$p$$ (e.g. 600 digits).

Fix an integer $$g$$ in $${1, …, p}$$.

$$B^a(mod \ p) = (g^b)^a = g^{ab}(mod \ p) = (g^a)^b = A^b(mod \ p)$$

• Option 4: Public Key Encryption

Definition: a public-key encryption system is a triple of algorithms $$(G, E, D)$$ where $$G()$$ is a randomized algorithm that outputs a key pair $$(pk, sk)$$, $$E(pk,m)$$ is a randomized algorithm that takes $$m ∈ M$$ (message) and outputs $$c ∈ C$$ (ciphertext), and $$D(sk, c)$$ is a determined algorithm that takes $$c ∈ C$$ and outputs $$m ∈ M$$ or ⊥.

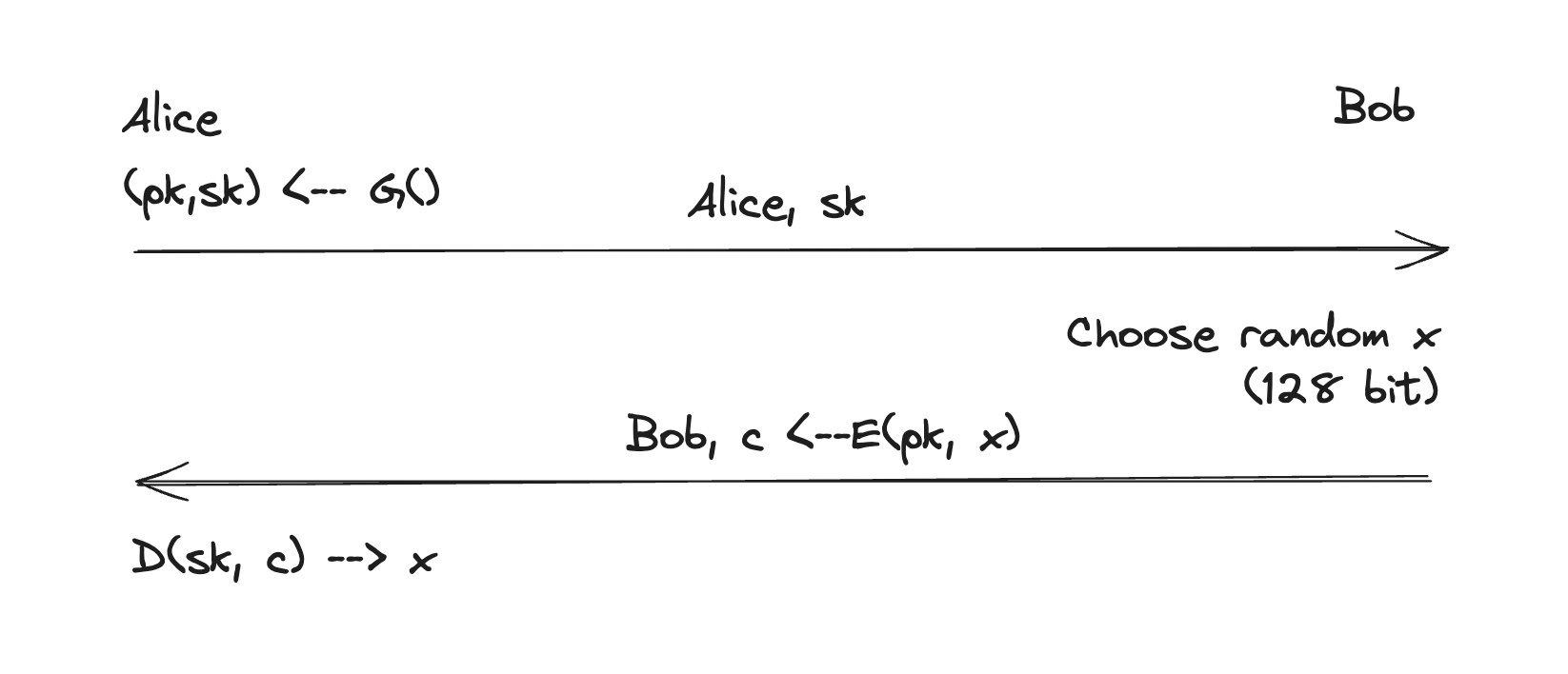
Public key encryption is very popular in modern world. For example, it is often used for session setup (establishing a communication session between two or more entities, such as clients and servers, in a networked environment) and non-interactive applications (e.g. email).

One of the most widely known public key encryption protocols is the RSA trapdoor permutation (1977) – it is used, for example, in SST/TSL protocols, secure emailing and file systems, etc.

Among other examples of public key encryption – ElGamal that relies on Diffie-Hellman protocol.

Data Encryption Standard and conclusions

The National Institute of Standards and Technology, also known as the NIST, is a United States government laboratory that works to develop, test, and recommend best practices for federal agencies, and other organizations relating to things such as online security. Metrics, measurements, and regulations, like the Federal Information Protection Standard, are created by the NIST to help strengthen the reliability and security of technologies being developed.

For Cryptographic Standards and Guidelines, check the NIST website.

One should mention that adopted as a standard doesn’t mean 100% secure forever. Though it means that a lot of great minds checked, explored, and researched the specific primitive and came to the conclusion that it is secure following a specific security definition for this specific primitive.

While more research is being conducted, hardware acceleration moves forwards, R&D in the quantum domain progresses, the cryptography landscape will change: new primitives will substitute previous generations. For example, using 256-bit keys instead of 128-bit ones.

And while cryptography is one of the most exciting and dynamically developing areas, it is also extremely complex and tricky. That is why, as recommended by Dan Boneh, it is better not to invent your own cryptography, not to write own implementations of already existing cryptography, and stick to existing standards. It doesn’t guarantee 100% security, however, it guarantees as good security as it is possible to achieve.

Sources

• This article mostly relies on the legendary Dan Boneh’s “Cryptography I”

• For definitions, wikipedia, investopedia, cloudflare, brilliant.org were used.

• csrc.nist.gov