Introduction
How can a Prover convince a Verifier that he can accurately compute the sum of the evaluation of a function $$g$$ over all possible inputs $${ 0,1 }$$ ?
Let's say the Prover has a function $$g$$ that takes several binary variables, $$b_1,b_2,…,b_l$$, where each variable can only be either $$0$$ or $$1$$. The goal is for the Prover to convince the Verifier that he can compute the sum of the function $$g$$ evaluated on all possible combinations of these binary inputs correctly without any malicious intent.
This sum would be:
$$$
C = \sum_{b_1,b_2,…,b_l \in { 0,1 }} g(b_1,b_2,…,b_l)
$$$
simplified to :
$$$
\sum_{b_1 \in { 0,1 }} \sum_{b_2 \in { 0,1 }} ... \sum_{b_l \in { 0,1 }} g(b_1,...,b_l)
$$$
However, instead of the Verifier recomputing everything to check if the Prover’s claim is correct (which could take too long if there are many variables), they use the sumcheck protocol.
For instance suppose we define the function $$g$$ :
$$$
g(b_1,b_2,b_3,b_4,b_5)= 2b^2_1+b_2+b_1b_2b_3-b_4+b_2b^3_5
$$$
As you can see below, this function has a different evaluation for all possible combination of 0 and 1 for the variables of $$b_1$$ to $$b_5$$.
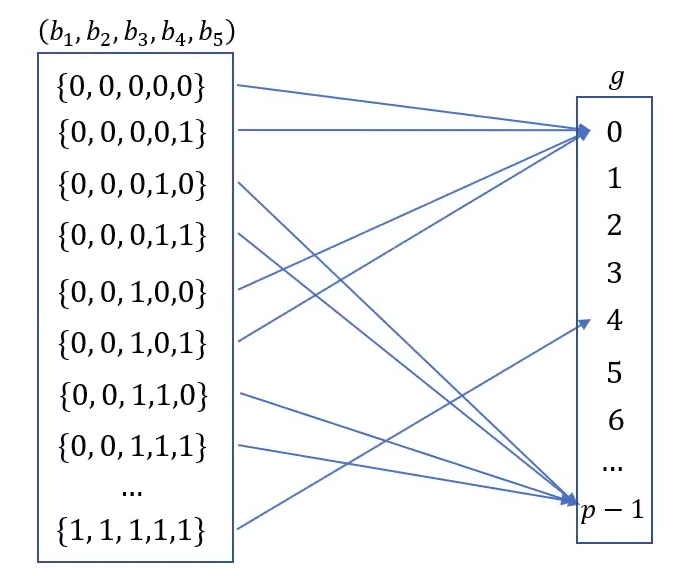
If the Prover has calculated the sum of all evaluations and combined them together by taking the result of $$g(b_1,b_2,b_3,b_4,b_5)$$ at every possible combination (32 combinations because $$2^5=32$$) and adding them up, it will amount to 44.
Quick demonstration:
If we replace $$g(b_1,b_2,b_3,b_4,b_5)$$ with $${ 0,0,0,0,0 }$$, we will get 0.
$$$
g(b_1,b_2,b_3,b_4,b_5)= 2b^2_1+b_2+b_1b_2b_3-b_4+b_2b^3_5
$$$
$$$
g(0,0,0,0,0) = 2 \times 0 + 0 + 0 \times 0 \times 0 - 0 + 0 \times 0 = 0
$$$
$$$
g(0,0,0,0,0) + g(0,0,0,0,1)+ ... + g(1,1,1,1,1) = 44
$$$
How can the Prover convince the verifier that the calculated value 44 is correct and has not been tampered with?
The naive solution is that the verifier could calculate the sum himself but this is time consuming, so we need a more efficient algorithm. The sum-check protocol provides a solution for this problem.
General Overview of Sumcheck Protocol
This is just a general overview, don’t worry if you don’t understand it. We’ll explain everything later so you skip it if you want.
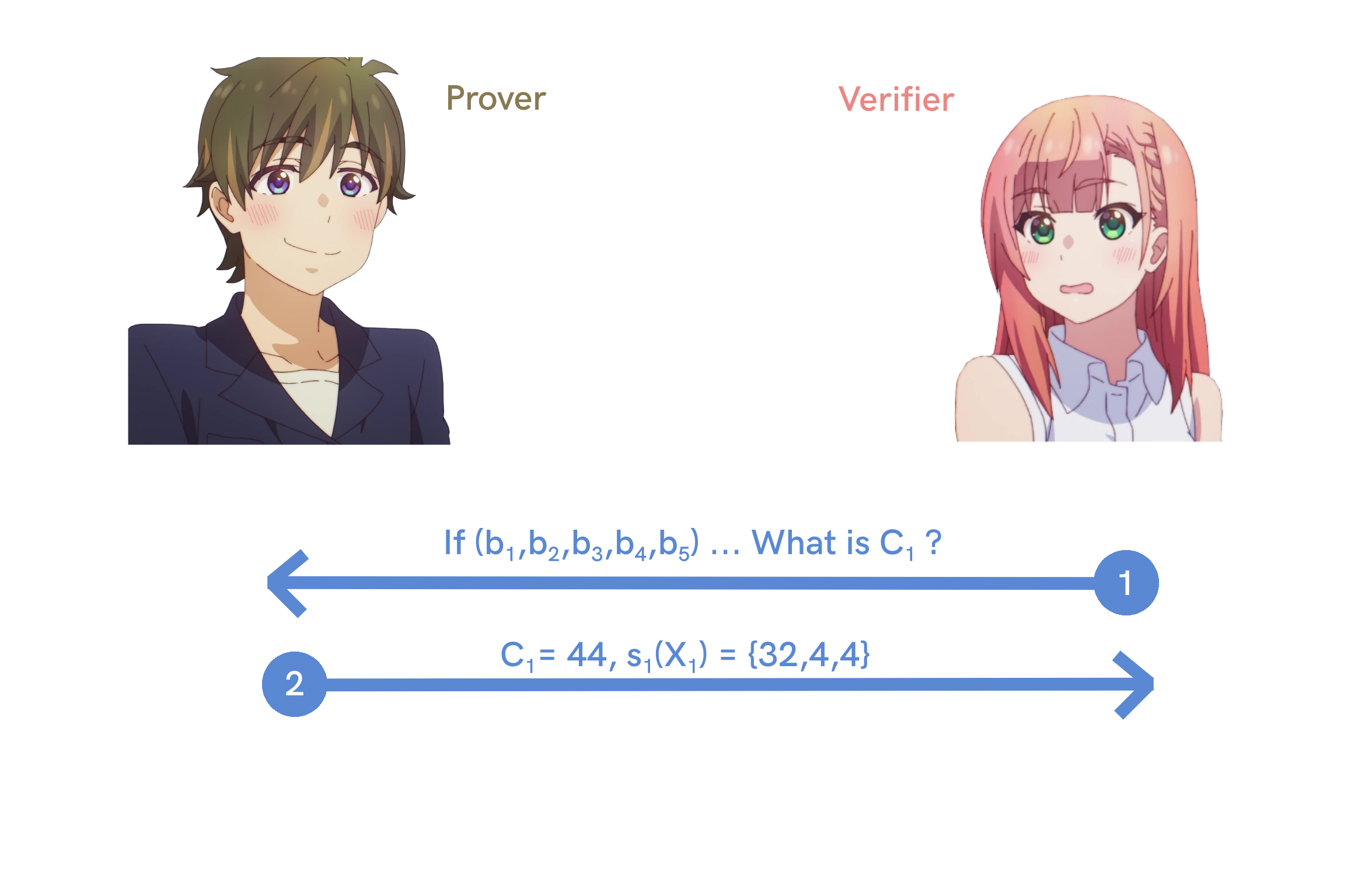
- Start : Prover sends claimed answer $$C_1$$ which in our previous example was 44. The protocol must check that :
$$$
C_1 = \sum_{b_1 \in {0,1 }} \sum_{b_2 \in{0,1}} ... \sum_{b_l \in {0,1 }} g(b_1,...,b_l)
$$$
- Round 1 : Prover sends univariate polynomial $$S_1(X_1)$$ claimed to equal :
$$$
H_1(X_1) = \sum_{b_2 \in{0,1}} ... \sum_{b_l \in {0,1 }} g(X_1,...,b_l)
$$$
$$s_1$$ what the prover actually sends and $$H_1$$ is what the prover would send if the prover is honest. Note that the degree of $$H_1$$ and $$X_1$$ is at most the degree of the multivariate $$g$$ in its first variable meaning that if $$g$$ has a low degree in each variable (for example : 2 or 3) then even though there are $$2^{l -1}$$ terms in this sum, $$H_1$$ will simply be a degree 2 or 3 univariate polynomial. Hence, specifying $$H_1$$ can be done by just sending three or 4 coefficients.
Verifier checks that $$C_1 = s_1(0) + s_1(1)$$. If this check passes, it is safe for the Verifier to assume that $$C_1$$ is the correct answer, so long as the Verifier believes that $$s_1 = H_1$$. How do we check that ? We just check that $$s_1$$ and $$H_1$$ agree at a random point $$r_1$$.
-
Round $$l$$ (Final Round): The Prover sends univariate polynomials $$s_l(X_l)$$ claimed to be equal :
$$$
H_l := g(r_1,...,r_{l-1},X_l)
$$$
Verifier checks that $$s_{l-1}(r_{l-1}) ] = s_l(0) + s_l(1)$$.
Verifier picks $$r_l$$ at random, and needs to check that $$s_l(r_l) = g(r_l,…,r_l)$$.
No need for more rounds, the verifier can perform this check with one oracle query. So after $$ l$$ rounds of interaction, the prover can convince the verifier.
Round One
In this example we will be sticking to our original function $$g$$:
$$$
\boxed {g(b_1,b_2,b_3,b_4,b_5)= 2b^2_1+b_2+b_1b_2b_3-b_4+b_2b^3_5}
$$$
Prover knows the function $$g(b_1,b_2,b_3,b_4,b_5)$$ and he wants to compute :
$$$
C_1 = \sum_{b_1 \in {0,1 }} \sum_{b_2 \in{0,1}} \sum_{b_3 \in {0,1 }}\sum_{b_4 \in {0,1 }}\sum_{b_5 \in {0,1 }} g(b_1,b_2,b_3,b_4,b_5)
$$$

In the first step, the Verifier shares the function with the Prover and ask him what the summation of all evaluations which is $$C_1$$.
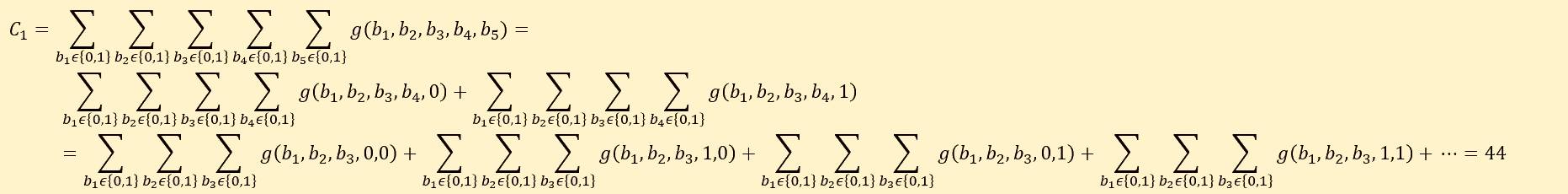
In the first round, the Prover calculates the required summation which is $$C_1$$. This means that the Prover needs to open the summation over all the variables of $$b_1$$ to $$b_5$$ for the values $$0$$ and $$1$$. For better comprehension, we can write the above image/function like this :
$$$
g(0,0,0,0,0) + g(0,0,0,0,1)+ ... + g(1,1,1,1,1) = 44
$$$
After the Prover has calculated the sum of all evaluations and combined them together, he will get the value 44 which is the required summation $$C_1$$.
Then the prover will have to share this value with the verifier. However only providing the value isn’t enough to satisfy the Verifier because she doesn’t know if the Prover has really done the work, has really calculated this summation properly. Thus some extra calculations need to be done and shared to satisfy the Verifier. We can’t upset the Verifier. The Prover might also need to buy her some flowers while he’s at it.
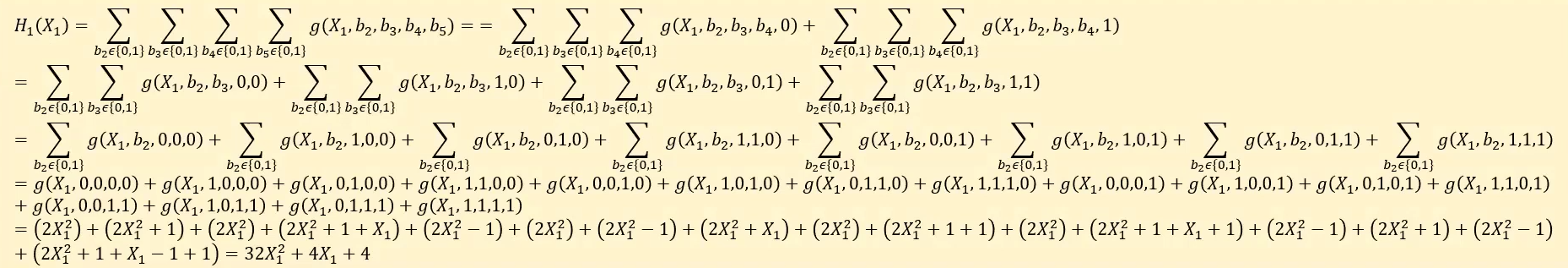
For the extra calculations, the Prover needs to define $$H_1X_1$$. This step is repetitive in different in every single interaction. So in each round the Prover has to form a function $$H_iX_i$$. In the first round, the Prover forms the function $$H_1X_1$$ by only swapping the first variable $$b_1$$ of function $$g$$, by $$X_1$$. This means that the Prover needs to hold this fixed variable and then calculate the summation based on the remaining variables $$b_2$$ to $$b_5$$. So each variable in the function g except $$X_1$$ can be either $$0$$ or $$1$$.
This computation leads a polynomial :
$$$
H_1(X_1) = 32X^2_1 + 4X_1 + 4
$$$
By assuming that the Prover is malicious and might not have shared the accurate function $$H_1(X_1)$$, we will need to use a different notation as $$s_1(X_1)$$.
$$s_1$$ what the prover actually sends and $$H_1$$ is what the prover would send if the prover is honest.
We expect that $$s_1$$ should be equal to $$H_1$$. The Prover later sends $$C_1$$ as the summation of the evaluation, the polynomial $$s_1(X_1)$$ and the coefficient of the polynomial $$32X^2_1+4X_1+4$$ which are $${32,4,4 }$$.
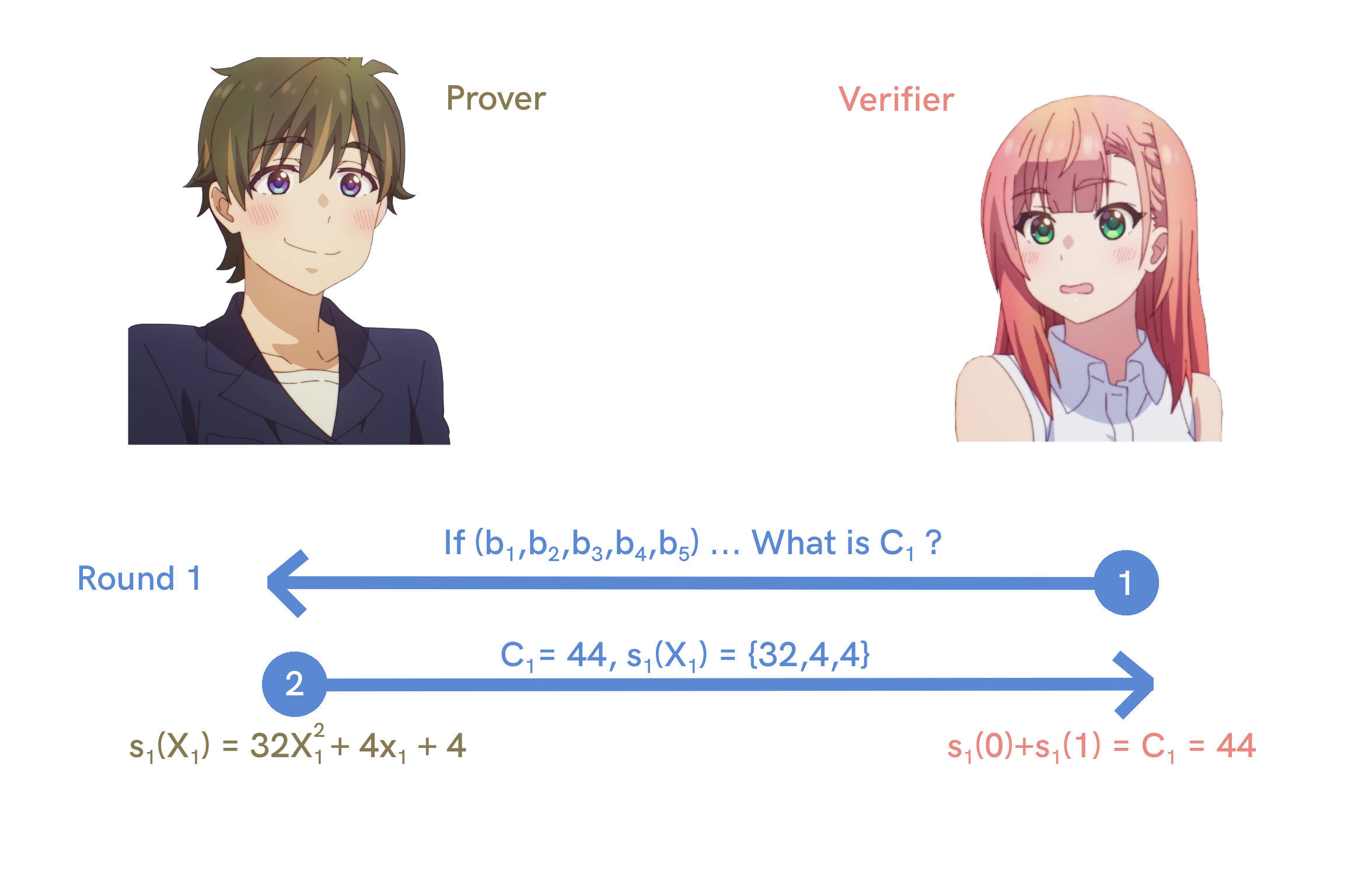
On the verification side, the Verifier forms $$s_1(X_1)$$ using the received coefficients and then calculates $$s_1(0)$$ which is 4.
So the Verifier replaces $$X_1$$ with 0 in the polynomial $$32X^2_1+4X1+4$$ which results to $$32×0+4×0+4=4$$ and she did the same thing with $$s_1(1)$$ = $$32 \times 1 + 4 \times 1 + 4 = 40$$
We can see the equation is correct because $$s_1(0)+s_1(1)= C_1 =44$$ meaning the first check is approved.
This is not enough to satisfy the Verifier so we need to perform a second round. I guess the Prover should have also bought her some chocolate. Let’s keep going and see what’s his second move.
Round Two
The prover takes the previous function and changes $$b_1$$ to $$r_1$$ and $$b_2$$ to $$X_2$$
$$$
\boxed {g(r_1,X_2,b_3,b_4,b_5)= 2r^2_1+X_2+r_1X_2b_3-b_4+X_2b^3_5}
$$$
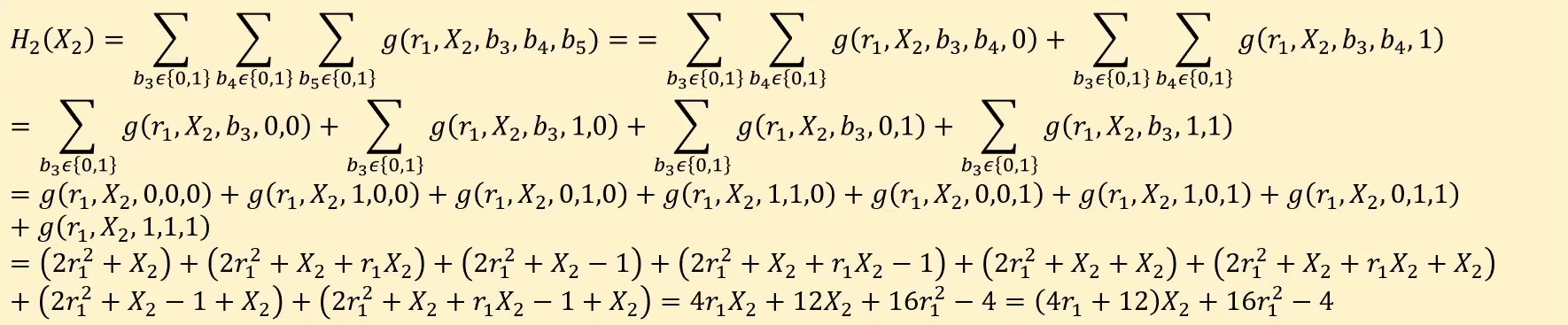
Then he proceeds to calculate the sum of all evaluations of function $$g(r_1,X_2,b_3,b_4,b_5)$$ over all possible values that consists of $$0$$ and $$1$$ for only $$b_3,b_4,b_5$$ and add them up to form a polynomial. This means that the Prover should not change $$r_1$$ and $$X_2$$ which are the first two variables to $$0$$ or $$1$$.
In the end, we will have a the equation :
$$$
(4r_1+12)X_2+16r^2_1-4
$$$
My guy has no rizz so she decided to give him a hint by sending him a random value $$r_1$$ equal to 93. He takes the random value $$r_1$$ and puts it in the equation above.
$$$
s_2(X_2) = (4 \times 93 +12)X_2+16 \times 93^2-4 = 352X_2+ 115596
$$$
The Prover was able to calculate $$s_2(X_2)$$ which is $$352X_2+ 115596$$ and similarly to the previous round the Prover should send the coefficient of the polynomial which is $${ 352,115596 }$$ to the Verifier (Bold move by the Prover).

On the verification side, the Verifier will calculate $$s_2(0) + s_2(1)$$ by changing $$X_2$$ to $$0$$ which gives us $$352 \times 0 + 115596 = 115596 = s_2(0)$$ and changing $$X_2$$ to $$1$$ which gives us $$352 \times 1 + 115596 = 115948 = s_2(1)$$.
$$$
s_2(0)+s_2(1) = 115596 + 115948 = 277144
$$$
In addition from the previous rounds, the Verifier knows the function $$s_1(X_1)$$so then the verifier could calculate the value of $$s_1(r_1)$$ by changing $$X_1$$ with $$r_1$$.
$$$
32X^2_1+4X_1+4 = 32 \times 93^2 + 4 \times 93 + 4 = 277144
$$$
So the sum of $$s_2(0)+s_2(1)$$ should be equal to $$s_1(r_1)$$. The second test passed.
The verifier is convinced that the Prover did everything right till now.
Bro is winning but she’s playing hard to get.
Bro needs to be persistent and patient.
Let’s see his next move!!
Round Three
Like last time, the Verifier chooses another random value $$r_2 = 35$$ and sends it to the Prover (What a lucky guy). The Prover generates an updated version of our original function by replacing $$b_1, b_2$$ and $$b_3$$ with $$r_1,r_2$$ and $$X_3$$.
$$$
\boxed {g(r_1,r_2,X_3,b_4,b_5) = 2r^2_1 + r_2 + r_1r_2X_3 - b_4 + r_2b^3_5}
$$$
He then proceeds to compute the function $$H_3(X_3)$$ by calculating the summation for the variables $$b_4$$ and $$b_5$$ which are the only two remaining values that should be replaced by $$0$$ and $$1$$.
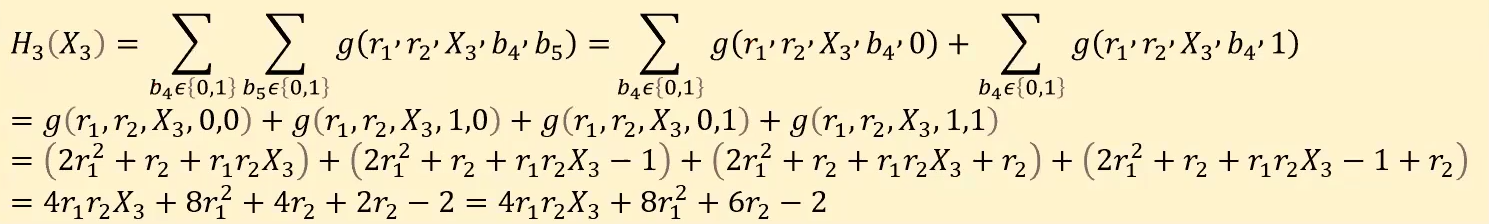
$$$
H_3(X_3) = s_3(X_3,r_2) = 4r_1r_2X_3 + 8r^2_1 + 6r_2 - 2
$$$
By replacing the values $$r_1 = 93$$ and $$r_2 = 35$$, the Prover will get :
$$$
s_3(X_3) = 13020X_3 + 69400
$$$
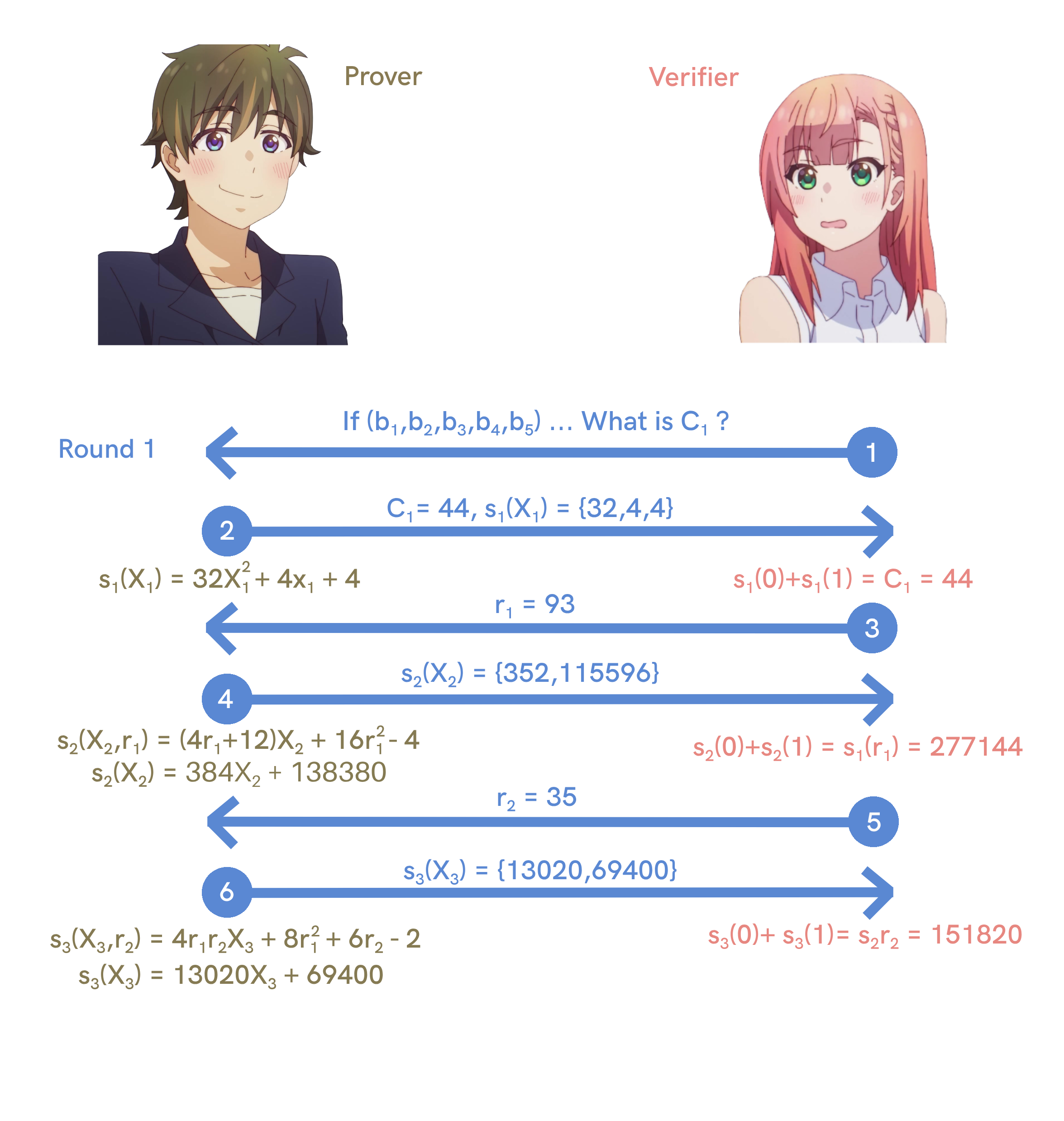
Then the Prover will share the coefficients $${ 13020,69400 }$$ of the polynomial $$s_3(X_3)$$ with the Verifier so she can calculate $$s_2(r_2)$$.
Since she knows the coefficients of $$s_2(X_2)$$, she can calculate $$s_2(r_2)$$ and get the same value as $$s_3(0)+s_3(1) = 151820$$.
You may be asking how can she calculate $$s_2(r_2)$$ with only the coefficients ?
The Verifier receives the coefficients in this format :
$$$
[0, 0, 0, 0, 384, 138380]
$$$
For more clarity, you can imagine the function $$s_2(r_2)$$ like this
$$$
[0(x^5), 0(x^4), 0(x^3), 0(x^2), 384(x), 138380]
$$$
So from the coefficients, the Verifier can construct $$s_2(r_2)$$:
$$$
s_2(r_2) = 384x^2 + 138380
$$$
and then replace $$r_2$$ with 35 :
$$$
s_2(35) = 384 \times 35^2 + 138380 = 151820
$$$
This can be done by replacing $$X_2$$ with $$r_2$$. So we just replace $$r_1$$ with 93 and $$r_2$$ with 35 :
$$$
(4r_1+12)X_2+16r^2_1-4 = (4 \times 93 + 12) \times 35 + 16 \times 93^2 - 4 = 151820
$$$
$$$
s_2(r_2) = s_3(0)+s_3(1) = 151820
$$$
If the two sides of the equation is correct then the next round passes.
Round Four
Round 4 is similar to round 2 and 3.

Round Five (Final Round)
I’d like to mention that we have 5 rounds of interaction between Prover and Verifier because we have 5 variables in the function $$g$$ → $$(b_1,b_2,b_3,b_4,b_5)$$.
5 Rounds of Interactions: (1,2), (3,4), (5,6), (7,8), (9,10).
So for the final round, the Verifier chooses a random value $$r_4$$. On the other side the Prover calculates the function g by replacing $$b_1$$ to $$b_5$$ by $$r_1,r_2,r_3,r_4,X_5$$
$$$
\boxed {g(r_1,r_2,r_3,r_4,X_5) = 2r^2_1 + r_2 + r_1r_2r_3 - r_4 + r_2X^3_5}
$$$
$$H_5(X_5)$$ is similar to $$g(r_1,r_2,r_3,r_4,X_5)$$ because there’s no remaining variables to be replaced by $$0$$ and $$1$$ to calculate any summation.
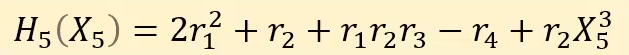
The Prover will replace the variables $$r_1$$ to $$r_4$$ in $$s_5(X_5,r_4)$$ to get :
$$$
35X^3_5 + 82407
$$$
and share the coefficients of the polynomial to the Verifier one last time .
The Verifier will calculate $$s_5(0) + s_5(1)$$ and check if its equal to $$s_4(r_4)$$ based on the coefficient received $$s_4$$ from the previous round and then the verifier.
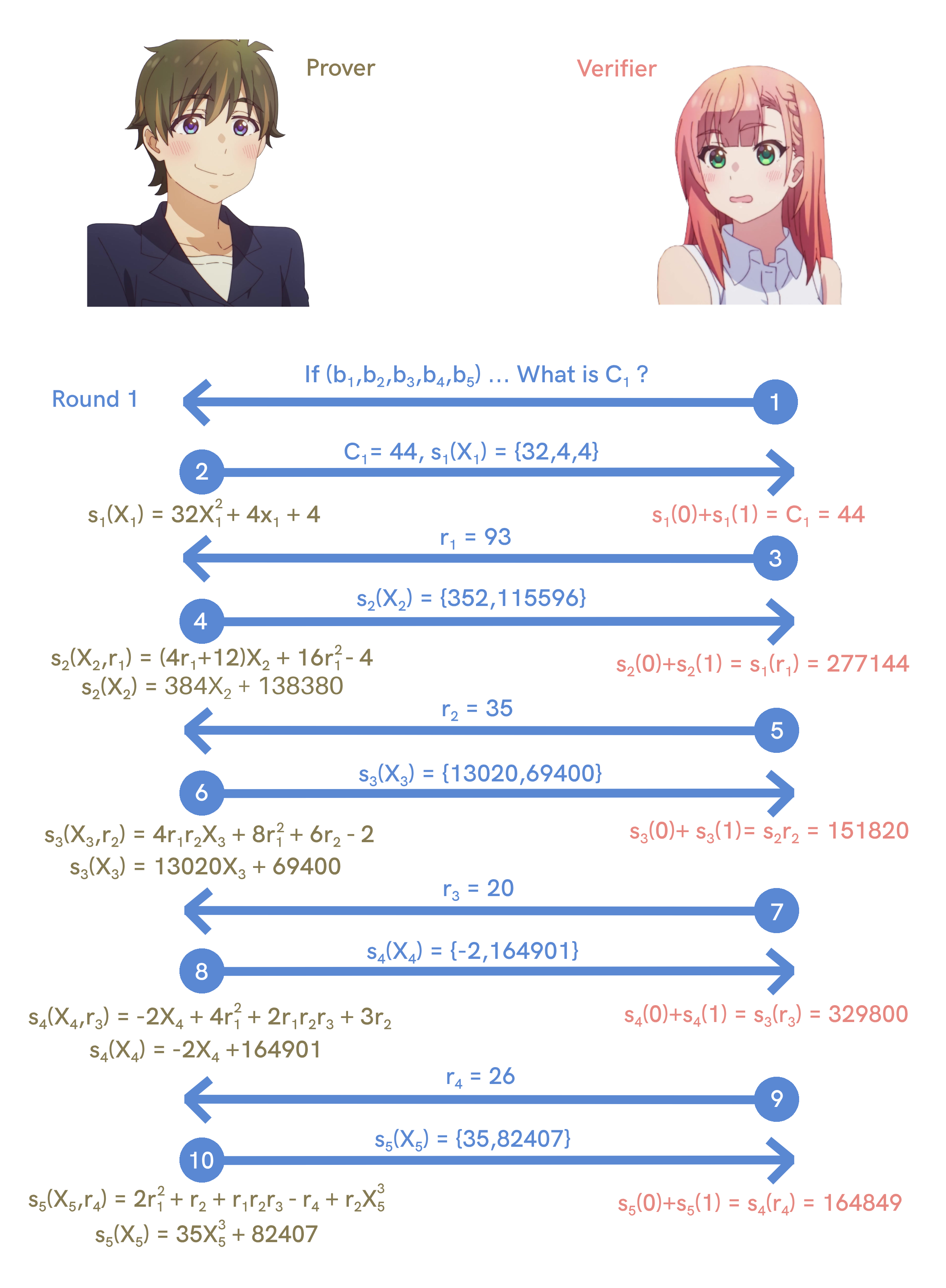
This can be done by replacing $$X_4$$ with $$r_4$$.
$$$
s_4(r_4) = -2r_4 + 164901 = -2 \times 26 + 164901 = 164849
$$$
So $$s_5(0) + s_5(1)$$ is equal to $$s_4(r_4)$$. The test passes!!
Last Check
The only thing left is to check if the final round passes. The verifier picks a random value $$r_5 = 14$$ and then she will need to calculate $$ g(r_1,r_2,r_3,r_4,r_5)$$.
Since the verifier knows the function $$g$$, she can replace the variables $$b_1$$ to $$b_5$$ by $$r_1$$ to $$r_5$$ and calculate $$s_5(r_5)$$ :
$$$
g(r_1,r_2,r_3,r_4,r_5) = s_5(r_5) = 2r^2_1 + r_2 + r_1r_2r_3 - r_4 + r_2r^3_5
$$$
$$$
g(93,35,20,26,14) = 2 \times 93^2 + 35 + 93 \times 55 \times 20 - 26 + 35 \times 14^3 = 178447
$$$
We then check $$s_5(r_5)$$ :
$$$
s_5(r_5) = 35r^3_5 + 82407 = 35 \times 14^3 + 81407 = 178447
$$$
Thus :
$$$
g(r_1,r_2,r_3,r_4,r_5) = s_5(r_5) = 178447
$$$
This means that the verifier is convinced that the first received value of $$C_1$$ which is 44 is the correct summation. Finally the Prover and Verifier are dating!!!!!
Conclusion
We can conclude that SumCheck Protocol needs $$l$$-rounds of interactions between Prover and Verifier to convince the Verifier that the summation was correctly computed. We can use Fiat-Shamir to make the SumCheck protocol non interactive.
Hope this was helpful and you finally understood the SumCheck Protocol. If you’re wondering there isn’t a season 2 for it so at least it was a happy ending.
Stay tuned for more !!




评论 (0)